题目内容
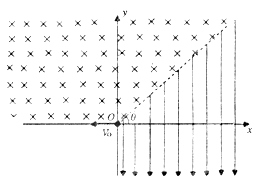
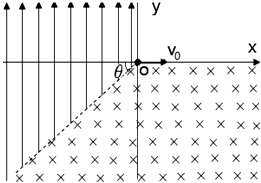在竖直平面内，以虚线为界分布着如图所示的匀强电场和匀强磁场，其中匀强电场方向向上，大小为E；匀强磁场垂直纸面向里，磁感应强度大小为B．虚线与水平线之间的夹角为θ=45°，一带电粒子从O点以速度v0水平射入匀强磁场，已知带负电粒子电荷量为q，质量为m，（重力忽略不计，电场、磁场区域足够大）．（1）求带电粒子第1次通过虚线时，粒子距O点的距离？
（2）当带电粒子第4次通过虚线时，求粒子距O点的距离和粒子经历的时间．
分析：（1）画出粒子运动的轨迹，根据洛伦兹力提供向心力求出运动半径，根据几何关系即可求解；
（2）粒子在磁场中做圆周运动，求出运动时间，第一次进入电场时做匀减速直线运动，求出运动时间，带电粒子将从B点反向加速重新进入磁场，再次求出运动的时间，带电粒子从C点再次进入电场中做类平抛运动，求出第四次进入磁场的时间，根据几何关系求解粒子距O点的距离．
（2）粒子在磁场中做圆周运动，求出运动时间，第一次进入电场时做匀减速直线运动，求出运动时间，带电粒子将从B点反向加速重新进入磁场，再次求出运动的时间，带电粒子从C点再次进入电场中做类平抛运动，求出第四次进入磁场的时间，根据几何关系求解粒子距O点的距离．
解答：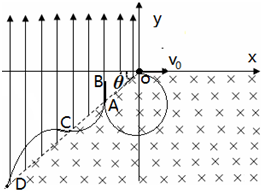
解：如图所示：
（1）带电粒子在磁场中运动半径为：r=
，
因为θ=45°，根据几何关系，带电粒子从O运动到A为
圆周，解得xOA=
r=
（2）因为T=
，带电粒子从O运动到A为
圆周，则带电粒子在磁场中运动时间为
t1=
T=
粒子从A点进入电场，受到电场力F=qE，则在电场中加速度大小为：a=
从A到B的时间为：tAB=
=
带电粒子将从B点反向加速重新进入磁场，由几何关系可知，带电粒子从A到C为
圆周，则：
再一次在磁场中运动t1=
T=
xAC=xOA=
带电粒子从C点再次进入电场中做类平抛运动
X=v0tCD
Y=
atCD2
Y=Xtanθ
得 tCD=
X=Y=
由于XCD=
=
所以第四次到电场与磁场分界虚线距O点距离为
△X=XOA+XAC+XCD=
第四次到达电场与磁场分界虚线的总时间为
t=t1+2tAB+t2+tCD=
+
答：（1）求带电粒子第1次通过虚线时，粒子距O点的距离为
；
（2）当带电粒子第4次通过虚线时，粒子距O点的距离为
，粒子经历的时间为
+
．
解：如图所示：（1）带电粒子在磁场中运动半径为：r=
| mv0 |
| Bq |
因为θ=45°，根据几何关系，带电粒子从O运动到A为
| 3 |
| 4 |
| 2 |
| ||
| Bq |
（2）因为T=
| 2πm |
| Bq |
| 3 |
| 4 |
t1=
| 3 |
| 4 |
| 3πm |
| 2Bq |
粒子从A点进入电场，受到电场力F=qE，则在电场中加速度大小为：a=
| qE |
| m |
从A到B的时间为：tAB=
| v0 |
| a |
| mv0 |
| qE |
带电粒子将从B点反向加速重新进入磁场，由几何关系可知，带电粒子从A到C为
| 1 |
| 4 |
再一次在磁场中运动t1=
| 1 |
| 4 |
| πm |
| 2Bq |
xAC=xOA=
| ||
| Bq |
带电粒子从C点再次进入电场中做类平抛运动
X=v0tCD
Y=
| 1 |
| 2 |
Y=Xtanθ
得 tCD=
| 2mv0 |
| qE |
X=Y=
| 2mv02 |
| qE |
由于XCD=
| X2+Y2 |
2
| ||
| qE |
所以第四次到电场与磁场分界虚线距O点距离为
△X=XOA+XAC+XCD=
2
| ||
| BqE |
第四次到达电场与磁场分界虚线的总时间为
t=t1+2tAB+t2+tCD=
| 2πm |
| Bq |
| 4mv0 |
| qE |
答：（1）求带电粒子第1次通过虚线时，粒子距O点的距离为
| ||
| Bq |
（2）当带电粒子第4次通过虚线时，粒子距O点的距离为
2
| ||
| BqE |
| 2πm |
| Bq |
| 4mv0 |
| qE |
点评：本题是带电粒子在组合场中运动的问题，粒子在电场中偏转做类平抛运动，在磁场中做匀速圆周运动，要求同学们能画出粒子运动的轨迹，结合几何关系求解，难度较大．
练习册系列答案
相关题目
（2011?株洲一模）在竖直平面内，以虚线为界分布着如图所示的匀强电场和匀强磁场，其中匀强电场方向向下，大小为E；匀强磁场垂直纸面向里，磁感应强度大小为B．虚线与水平线之间的夹角为θ=45°，一带电粒子以速度v0水平射入匀强磁场，已知带负电粒子电荷量为q，质量为m，（重力忽略不计，电场、磁场区域足够大）．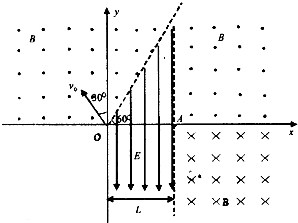
在竖直平面内，以虚线为界分布着如图所示的匀强电场和足够大的匀强磁场，各区域磁场的磁感应强度大小均为B，匀强电场方向竖直向下，大小为E=
