题目内容
14．甲．乙两物体同时由同一地点向同一方向作直线运动，其υ-t图象如图所示，下列说法正确的是（ ）
| A． | 20s末甲、乙两物体间相遇 | |
| B． | 前20s内甲、乙两物体间的距离逐渐增大 | |
| C． | 前40s内甲、乙两物体间距离一直在增大，40s末达到最大 | |
| D． | 前40s内甲、乙两物体间的距离先增大后减小，40s末乙追上甲 |
分析 在速度时间图象中，某一点代表此时刻的瞬时速度，时间轴上方速度是正数，时间轴下方速度是负数；切线代表该位置的加速度，向右上方倾斜，加速度为正，向右下方倾斜加速度为负；图象与坐标轴围成面积代表位移，时间轴上方位移为正，时间轴下方位移为负，交点表示速度相同，此时相距最远．
解答 解：A、甲、乙两物体同时由同一地运动，相遇时位移相同，所以在40s末甲乙两物体面积（位移）相同，此时相遇，故A错误．
BCD、前20s内甲物体速度大、乙的速度小，所以两物体间的距离逐渐增大，20s-40s内，后方物体乙速度大，两物体间距减小，到40s末位移相同，相遇．故C错误，BD正确．
故选：BD
点评 本题是为速度--时间图象的应用，要明确斜率的含义，知道在速度--时间图象中图象与坐标轴围成的面积的含义．
练习册系列答案
相关题目
4．在“探究导体电阻与其影响因素的定量关系”实验中，器材有：
a．粗细均匀的金属丝（长度x为1.1m，总电阻约5Ω）
b．直流电源（1.5V，内阻不计）
c．电流表（量程0.6A，内阻约为1Ω）
d．电流表（量程300mA，内阻约为2Ω）
e．电压表（1.5V，内阻约3kΩ）
f．滑动变阻器（10Ω，1.0A）
g．定值电阻（5.0Ω，1.0A）
h．刻度尺、开关、导线若干
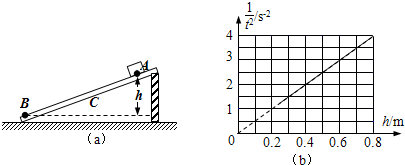
为丁探究金属丝的电阻与长度的关系，甲、乙两位同学选择以上部分器材设计如图（a）所示电路：
甲同学逐渐减小金属丝接入电路的长度x，调整滑动变阻器的触头位置，同时保持电压表示数不变，读出对应的电流表示数，通过计算得到金属丝电阻R甲．得到具体数据如表格一所示．
乙同学逐渐减小金属丝接入电路的长度x，调整滑动变阻器的触头位置，同时保持电流表示数不变，读出对应的电压表示数，通过计算得到金属丝电阻R乙．得到具体数据如表格二所示，乙同学根据实验数据在坐标纸内画出R-x图钱，如图（b）所示．
（1）在乙同学所描图线的R-x图（答题卷的R～x图）中，根据甲同学的实验数据描出R-x图线（c）．
（2）乙同学应选电流表d（填器材序号，如a、b、C等）
（3）结合R-x图分析甲、乙两位同学的测量方案谁更合理，并简要说明原因．乙同学更合理，甲同学在电压不变的情况下，阻值减小，电流增大，温度有明显升高，金属丝电阻率发生明显变化，而乙同学方案保持电流不变，较好维持金属丝温度不变；
（4）若甲同学在保持电压不变的测量方案下，为了尽量减少温度变化对实验造成的影响，从题中给出的器材中选择所需器材，并设计改进电路？将改进后的电路图（c）画在答虚线框中，并在各元件旁标上它的器材序号．
a．粗细均匀的金属丝（长度x为1.1m，总电阻约5Ω）
b．直流电源（1.5V，内阻不计）
c．电流表（量程0.6A，内阻约为1Ω）
d．电流表（量程300mA，内阻约为2Ω）
e．电压表（1.5V，内阻约3kΩ）
f．滑动变阻器（10Ω，1.0A）
g．定值电阻（5.0Ω，1.0A）
h．刻度尺、开关、导线若干
为丁探究金属丝的电阻与长度的关系，甲、乙两位同学选择以上部分器材设计如图（a）所示电路：
甲同学逐渐减小金属丝接入电路的长度x，调整滑动变阻器的触头位置，同时保持电压表示数不变，读出对应的电流表示数，通过计算得到金属丝电阻R甲．得到具体数据如表格一所示．
| 表格一 | 金属丝长度/cm | 20.0 | 40.0 | 60.0 | 80.0 | 100.0 |
| 金属丝电阻/Ω | 2.2 | 2.6 | 3.2 | 4.0 | 5.0 |
| 表格二 | 金属丝长度/cm | 20.0 | 40.0 | 60.0 | 80.0 | 100.0 |
| 金属丝电阻/Ω | 1.0 | 2.1 | 3.0 | 3.9 | 5.0 |
（1）在乙同学所描图线的R-x图（答题卷的R～x图）中，根据甲同学的实验数据描出R-x图线（c）．
（2）乙同学应选电流表d（填器材序号，如a、b、C等）
（3）结合R-x图分析甲、乙两位同学的测量方案谁更合理，并简要说明原因．乙同学更合理，甲同学在电压不变的情况下，阻值减小，电流增大，温度有明显升高，金属丝电阻率发生明显变化，而乙同学方案保持电流不变，较好维持金属丝温度不变；
（4）若甲同学在保持电压不变的测量方案下，为了尽量减少温度变化对实验造成的影响，从题中给出的器材中选择所需器材，并设计改进电路？将改进后的电路图（c）画在答虚线框中，并在各元件旁标上它的器材序号．
5．下列说法中正确的是（ ）
| A． | 根据磁感应强度B的定义式B=$\frac{F}{IL}$可知，磁感应强度B与F成正比，与IL成反比 | |
| B． | 穿过某一回路的磁通量变化越快，产生感应电动势一定越大 | |
| C． | 由E=$\frac{F}{q}$知，若q减半，则该处电场强度为原来的2倍 | |
| D． | 磁场中某处磁感应强度的方向，与通电导线在该处所受磁场力的方向相同 |
2．
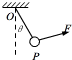如图所示，将质量为m的小球P用细线悬挂于O点，用拉力F拉住小球P使其处于静止状态，要求悬线与竖直方向成θ=30°角．拉力F的最小值为（ ）
如图所示，将质量为m的小球P用细线悬挂于O点，用拉力F拉住小球P使其处于静止状态，要求悬线与竖直方向成θ=30°角．拉力F的最小值为（ ）| A． | $\frac{\sqrt{3}}{2}$mg | B． | $\frac{1}{2}$mg | C． | $\frac{\sqrt{3}}{2}$mg | D． | mg |
6．
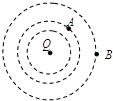如图，在点电荷Q产生的电场中，将两个带正电的试探电荷q1、q2分别置于A、B两点，虚线为等势线．取无穷远处为零电势点，若将q1、q2移动到无穷远的过程中外力克服电场力做的功相等，则下列说法正确的是（ ）
如图，在点电荷Q产生的电场中，将两个带正电的试探电荷q1、q2分别置于A、B两点，虚线为等势线．取无穷远处为零电势点，若将q1、q2移动到无穷远的过程中外力克服电场力做的功相等，则下列说法正确的是（ ）| A． | A点电势高于B点电势 | |
| B． | A、B两点的电场强度相等 | |
| C． | q1的电荷量小于q2的电荷量 | |
| D． | q1在A点的电势能小于q2在B点的电势能 |
3．
如图，足够大的光滑绝缘水平面上有三个带电质点，A和C围绕B做匀速圆周运动，B恰能保持静止，其中A、C和B的距离分别是L1，和L2．不计三质点间的万有引力，则A和C的比荷（电量与质量之比）之比应是（ ）
如图，足够大的光滑绝缘水平面上有三个带电质点，A和C围绕B做匀速圆周运动，B恰能保持静止，其中A、C和B的距离分别是L1，和L2．不计三质点间的万有引力，则A和C的比荷（电量与质量之比）之比应是（ ）| A． | （$\frac{{L}_{1}}{{L}_{2}}$）2 | B． | （$\frac{{L}_{1}}{{L}_{2}}$）3 | C． | （$\frac{{L}_{2}}{{L}_{1}}$）2 | D． | （$\frac{{L}_{2}}{{L}_{1}}$）3 |
4．
如图，甲图中虚线是点电荷产生的电场的等势面，乙图是匀强电场．电场中各有两点M、N，则（ ）
如图，甲图中虚线是点电荷产生的电场的等势面，乙图是匀强电场．电场中各有两点M、N，则（ ）| A． | 甲图中M、N两点的E相同，φ也相同 | |
| B． | 乙图中M、N两点的E相同，φ也相同 | |
| C． | 甲图中，带电粒子在M、N两点间移动，电场力做功为零 | |
| D． | 乙图中，带电粒子在M、N两点间移动，电场力做功为零 |