题目内容
6. 如图,光滑水平直轨道上有三个质量均为m的物块A、B、C. B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计).设A以速度v0朝B运动,压缩弹簧;当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动.假设B和C碰撞过程时间极短.求从A开始压缩弹簧直至与弹簧分离的过程中,
如图,光滑水平直轨道上有三个质量均为m的物块A、B、C. B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计).设A以速度v0朝B运动,压缩弹簧;当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动.假设B和C碰撞过程时间极短.求从A开始压缩弹簧直至与弹簧分离的过程中,(i)整个系统损失的机械能;
(ii)弹簧被压缩到最短时的弹性势能.
分析 (i)A压缩弹簧的过程,系统动量守恒,应用动量守恒定律可以求出A、B相等的速度.此时B与C发生完全非弹性碰撞,由动量守恒定律求出碰后共同速度.再由能量守恒定律可以求出损失的机械能.
(ii)系统动量守恒,由动量守恒定律求出三个物体共同速度,然后应用能量守恒定律可以求出弹簧的弹性势能.
解答 解:(i)从A压缩弹簧到A与B具有相同速度v1时,对A、B与弹簧组成的系统,取水平向右为正方向,由动量守恒定律得
mv0=2mv1 ①
此时B与C发生完全非弹性碰撞,设碰撞后的瞬时速度为v2,损失的机械能为△E.对B、C组成的系统,取水平向右为正方向,由动量守恒和能量守恒定律得
mv1=2mv2 ②
$\frac{1}{2}$mv12=△E+$\frac{1}{2}$•2mv22 ③
联立①②③式得:
整个系统损失的机械能为△E=$\frac{1}{16}$mv02 ④
(ii)由②式可知v2<v1,A将继续压缩弹簧,直至A、B、C三者速度相同,设此时速度为v3,此时弹簧被压缩至最短,其弹性势能为Ep.由动量守恒和能量守恒定律得
mv0=3mv3,⑤
由能量守恒定律得:
$\frac{1}{2}$mv02-△E=$\frac{1}{2}$•3mv32+EP ⑥
联立④⑤⑥式得
解得:EP=$\frac{13}{48}$mv02;
答:
(i)整个系统损失的机械能是$\frac{1}{16}$mv02;
(ii)弹簧被压缩到最短时的弹性势能是$\frac{13}{48}$mv02.
点评 本题综合考查了动量守恒定律和能量守恒定律,关键合理地选择研究的系统,知道弹簧被压缩到最短时三个物体速度相同,运用动量守恒和能量守恒进行研究.


| A. | 加5 V电压时,导体的电阻约是5Ω | |
| B. | 加12 V电压时,导体的电阻约是1.4Ω | |
| C. | 由图可知随着电压的增大,导体的电阻不断减小 | |
| D. | 由图可知随着电压的减小,导体的电阻不断减小 |
| A. | 40 m | B. | 50 m | C. | 32 m | D. | 60 m |
| A. | 火星的密度约为地球密度的$\frac{9}{8}$ | |
| B. | 火星上的第一宇宙速度约为地球上第一宇宙速度的$\frac{\sqrt{2}}{3}$ | |
| C. | 火星表面的重力加速度等于地球表面的重力加速度 | |
| D. | 火星表面的重力加速度约为地球表面的重力加速度的$\frac{9}{4}$ |
 如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )| A. | 物体的实际运动速度为v1+v2 | B. | 物体相对地面做曲线运动 | ||
| C. | 绳索始终保持竖直状态 | D. | 物体实际运动方向始终竖直向上 |
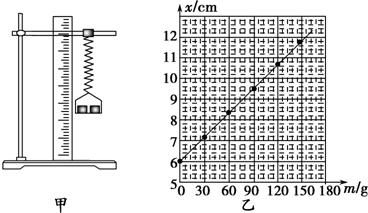
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 钩码质量m/g | 0 | 30 | 60 | 90 | 120 | 150 |
| 刻度尺读数/cm | 6.00 | 7.14 | 8.34 | 9.48 | 10.64 | 11.79 |
(2)作出的图线与坐标系纵轴有一截距,其物理意义是未挂钩码时弹簧的长度;该弹簧的劲度系数k=25.0N/m(结果保留3位有效数字).
(3)请你判断该同学得到的劲度系数与考虑砝码盘的质量相比,结果相同(填“偏大”、“偏小”或“相同”).
 某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:
某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:(A)表面光滑的长木板(长度为L),
(B)小车,
(C)质量为m的钩码若干个,
(D)方木块(备用于垫木板),
(E)米尺,
(F)秒表.
(1)实验过程:
第一步,在保持斜面倾角不变时,探究加速度与质量的关系.
实验中,通过向小车放入钩码来改变物体质量,只要测出小车由斜面顶端滑至底端所用时间t,就可以由公式a=$\frac{2L}{{t}^{2}}$求出a.某同学记录了数据如表所示:
 | M | M+m | M+2m |
| 1 | 1.42 | 1.41 | 1.42 |
| 2 | 1.40 | 1.42 | 1.39 |
| 3 | 1.41 | 1.38 | 1.42 |
第二步,在物体质量不变时,探究加速度与倾角的关系.实验中通过改变方木块垫放位置来调整长木板的倾角,由于没有量角器,因此通过测量出木板顶端到水平面高度h,求出倾角α的正弦值sinα=$\frac{h}{L}$.某同学记录了高度和加速度的对应值,并在坐标纸上建立适当的坐标轴后描点作图如图,请根据他所作的图线求出当地的重力加速度g=10m/s2.进一步分析可知,光滑斜面上物体下滑的加速度与倾角的关系为a=gsinα.

 一质点作简谐振动,它离开平衡的位移s(厘米)与时间t(秒)的关系为s=10sin(6πt+$\frac{π}{6}$).
一质点作简谐振动,它离开平衡的位移s(厘米)与时间t(秒)的关系为s=10sin(6πt+$\frac{π}{6}$).