题目内容
1.火星的半径约为地球半径的一半,质量约为地球质量的$\frac{1}{9}$,那么( )| A. | 火星的密度约为地球密度的$\frac{9}{8}$ | |
| B. | 火星上的第一宇宙速度约为地球上第一宇宙速度的$\frac{\sqrt{2}}{3}$ | |
| C. | 火星表面的重力加速度等于地球表面的重力加速度 | |
| D. | 火星表面的重力加速度约为地球表面的重力加速度的$\frac{9}{4}$ |
分析 根据$ρ=\frac{M}{V}$求解密度之比,根据g=$\frac{GM}{{R}^{2}}$求解重力加速度之比,根据v=$\sqrt{gR}$求解第一宇宙速度之比.
解答 解:A、密度$ρ=\frac{M}{V}$=$\frac{M}{\frac{4}{3}π{R}^{3}}$,故$\frac{{ρ}_{火}}{{ρ}_{地}}=\frac{{M}_{火}}{{M}_{地}}•(\frac{{R}_{地}}{{R}_{火}})^{3}=\frac{8}{9}$,故A错误;
B、第一宇宙速度v=$\sqrt{gR}$,故$\frac{{v}_{火}}{{v}_{地}}=\sqrt{\frac{{g}_{火}}{{g}_{地}}•\frac{{R}_{火}}{{R}_{地}}}=\sqrt{\frac{4}{9}×\frac{1}{2}}=\frac{\sqrt{2}}{3}$,故B正确;
CD、重力加速度g=$\frac{GM}{{R}^{2}}$,故$\frac{{g}_{火}}{{g}_{地}}=\frac{{M}_{火}}{{M}_{地}}•(\frac{{R}_{地}}{{R}_{火}})^{2}=\frac{4}{9}$,故CD错误;
故选:B
点评 本题考查万有引力定律的应用,根据万有引力定律得出重力加速度的决定式、第一宇宙速度的表达式是关键,也可以记住基本公式.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
2. 如图所示,平行板电容器两极板水平放置,电容为C,开始开关闭合,电容器与一直流电源相连,极板间电压为U,两极板间距为d,电容器储存的能量E=$\frac{1}{2}$CU2.一电荷量大小为q的带电油滴以初动能Ek从一平行板电容器的两个极板中央水平射入(极板足够长),带电油滴恰能沿图中所示水平虚线匀速通过电容器,则( )
如图所示,平行板电容器两极板水平放置,电容为C,开始开关闭合,电容器与一直流电源相连,极板间电压为U,两极板间距为d,电容器储存的能量E=$\frac{1}{2}$CU2.一电荷量大小为q的带电油滴以初动能Ek从一平行板电容器的两个极板中央水平射入(极板足够长),带电油滴恰能沿图中所示水平虚线匀速通过电容器,则( )
 如图所示,平行板电容器两极板水平放置,电容为C,开始开关闭合,电容器与一直流电源相连,极板间电压为U,两极板间距为d,电容器储存的能量E=$\frac{1}{2}$CU2.一电荷量大小为q的带电油滴以初动能Ek从一平行板电容器的两个极板中央水平射入(极板足够长),带电油滴恰能沿图中所示水平虚线匀速通过电容器,则( )
如图所示,平行板电容器两极板水平放置,电容为C,开始开关闭合,电容器与一直流电源相连,极板间电压为U,两极板间距为d,电容器储存的能量E=$\frac{1}{2}$CU2.一电荷量大小为q的带电油滴以初动能Ek从一平行板电容器的两个极板中央水平射入(极板足够长),带电油滴恰能沿图中所示水平虚线匀速通过电容器,则( )| A. | 保持开关闭合,将上极板下移$\frac{d}{3}$,带电油滴仍能沿水平线运动 | |
| B. | 保持开关闭合,将上极板下移$\frac{d}{3}$,带电油滴将撞击上极板,撞击上极板时的动能为Ek+$\frac{qU}{12}$ | |
| C. | 断开开关,将上极板上移$\frac{d}{3}$,带电油滴将撞击下极板,撞击下极板时的动能为Ek+$\frac{qU}{8}$ | |
| D. | 断开开关,将上极板上移$\frac{d}{3}$,若不考虑电容器极板的重力势能变化,外力对极板做功至少为$\frac{1}{6}$CU2 |
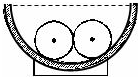 如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)
如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)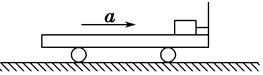 如图,一木块通过长度忽略不计的绳固定在小车的前壁上,小车上表面光滑.某时刻小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,滑块相对小车前3s内滑行了4.5m;后3s内滑行了10.5m.
如图,一木块通过长度忽略不计的绳固定在小车的前壁上,小车上表面光滑.某时刻小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,滑块相对小车前3s内滑行了4.5m;后3s内滑行了10.5m. 如图所示,一段长为a,宽为b,高为c(a>b>c)的导体,将其中的两个对立面接入电路中时,最大的电阻为R,则最小的电阻为$\frac{{c}^{2}R}{{a}^{2}}$.
如图所示,一段长为a,宽为b,高为c(a>b>c)的导体,将其中的两个对立面接入电路中时,最大的电阻为R,则最小的电阻为$\frac{{c}^{2}R}{{a}^{2}}$. 如图所示,小球以6m/s的速度由足够长的斜面中部沿着斜面向上滑.已知小球在斜面上运动的加速度大小为2m/s2,则小球的速度大小何时达到3m/s?(小球在光滑斜面上运动时,加速度的大小、方向都不改变)
如图所示,小球以6m/s的速度由足够长的斜面中部沿着斜面向上滑.已知小球在斜面上运动的加速度大小为2m/s2,则小球的速度大小何时达到3m/s?(小球在光滑斜面上运动时,加速度的大小、方向都不改变) 如图,光滑水平直轨道上有三个质量均为m的物块A、B、C. B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计).设A以速度v0朝B运动,压缩弹簧;当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动.假设B和C碰撞过程时间极短.求从A开始压缩弹簧直至与弹簧分离的过程中,
如图,光滑水平直轨道上有三个质量均为m的物块A、B、C. B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计).设A以速度v0朝B运动,压缩弹簧;当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动.假设B和C碰撞过程时间极短.求从A开始压缩弹簧直至与弹簧分离的过程中,
