题目内容
9．一小船在静水中的速率是5m/s，要渡过河宽为30m，水流速度为4m/s的河流，小船要以最短位移过河，则渡河的时间需要6s．分析 当静水速与河岸垂直时，渡河时间最短，由位移与速度的关系，即可求出时间．
解答 解：当静水速与河岸垂直时，垂直于河岸方向上的分速度最大，则渡河时间最短，
最短时间为：t=$\frac{d}{{v}_{c}}$=$\frac{30}{5}$s=6s；
故答案为：6．
点评 解决本题的关键知道合运动与分运动具有等时性，当静水速与河岸垂直，渡河时间最短；当合速度与河岸垂直，渡河航程最短．
练习册系列答案
相关题目
11．
汽车在拱桥上匀速率行驶，当汽车由拱桥的最高点A行驶到最低点B的过程中，下列说法不正确的是（ ）
汽车在拱桥上匀速率行驶，当汽车由拱桥的最高点A行驶到最低点B的过程中，下列说法不正确的是（ ）| A． | 支持力不做功 | B． | 重力不做功 | C． | 摩擦力作负功 | D． | 牵引力做正功 |
20．
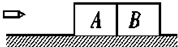如图所示，在光滑水平面上静止放着两个相互接触的木块A、B，质量分别为m 1和m 2，今有一子弹水平穿过两木块．设子弹穿过木块A、B的时间分别为t1和t2，木块对子弹的阻力恒为f，则子弹穿过两木块后，木块A、B的速度大小分别是（ ）
如图所示，在光滑水平面上静止放着两个相互接触的木块A、B，质量分别为m 1和m 2，今有一子弹水平穿过两木块．设子弹穿过木块A、B的时间分别为t1和t2，木块对子弹的阻力恒为f，则子弹穿过两木块后，木块A、B的速度大小分别是（ ）| A． | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ | |
| B． | $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$+$\frac{f{t}_{2}}{{m}_{2}}$ | |
| C． | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f（{t}_{1}+{t}_{2}）}{{m}_{1}+{m}_{2}}$ | |
| D． | $\frac{f（{t}_{1}+{t}_{2}）}{{m}_{1}}$ $\frac{f（{t}_{1}+{t}_{2}）}{{m}_{1}+{m}_{2}}$ |
17．
质量为m的物块，沿着半径为R的半球形金属壳内壁滑下，半球形金属壳竖直放置，开口向上，滑到最低点时速度大小为v，若物体与球壳之间的摩擦因数为μ，则物体在最低点时，下列说法正确的是（ ）
质量为m的物块，沿着半径为R的半球形金属壳内壁滑下，半球形金属壳竖直放置，开口向上，滑到最低点时速度大小为v，若物体与球壳之间的摩擦因数为μ，则物体在最低点时，下列说法正确的是（ ）| A． | 受到向心力大小为mg+m$\frac{{v}^{2}}{R}$ | B． | 受到支持力为mg+m$\frac{{v}^{2}}{R}$ | ||
| C． | 受到的摩擦力为μmg | D． | 受到的摩擦力为μm$\frac{{v}^{2}}{R}$ |
4．如图要使图中ab导线中有向右的电流，则金属棒MN应（ ）
| A． | 向右加速运动 | B． | 向左加速运动 | C． | 向右减速运动 | D． | 向左减速运动 |
14．
一个物体受到相互垂直的两个力的作用F1和F2作用下，物体发生了一段位移，F1对物体所做的功6J，F2对物体所做的功8J，则F1和F2的合力所做的功为（ ）
一个物体受到相互垂直的两个力的作用F1和F2作用下，物体发生了一段位移，F1对物体所做的功6J，F2对物体所做的功8J，则F1和F2的合力所做的功为（ ）| A． | .8 J | B． | 10 J | C． | 12 J | D． | 14 J |
1．如图所示是一个正弦式交变电流的图象，下列说法正确的是（ ）
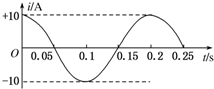
| A． | 周期是0.2 s，电流的峰值是10$\sqrt{2}$A | B． | 周期是0.25 s，电流的峰值是10 A | ||
| C． | 频率是5 Hz，电流的有效值是10 A | D． | 频率是5 Hz，电流的有效值是5$\sqrt{2}$A |