题目内容
14.如图甲为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量Φ随时间t按图乙所示正弦规律变化.求:
(1)交流发电机产生的电动势的最大值;
(2)电路中交流电压表的示数;
(3)线圈从图示位置开始转动90°的过程中通过电阻R的电量.
分析 (1)交流发电机产生电动势的最大值Em=nBSω,根据Φ-t图线得出周期T以及磁通量的最大值Φ=BS.从而求出感应电动势的最大值.
(2)交流电压表的示数为有效值,求出电动势的有效值,根据闭合电路欧姆定律求出电压表的示数.
(3)根据平均电动势求出平均电流,再由It即可求出电量.
解答 解:(1)由图可知,每匝线圈磁通量的最大值为${φ_m}=BS=2.0×{10^{-2}}Wb$
线圈转动的周期为T=6.28×10-2s
发电机产生的电动势最大值为${E_m}=nBSω=n{φ_m}\frac{2π}{T}=100×2.0×{10^{-2}}×\frac{2π}{{6.28×{{10}^{-2}}}}V=200V$
(2)由闭合电路的欧姆定律,可得感应电流的最大值${I_m}=\frac{E_m}{R+r}=\frac{200}{90+10}A=2A$
感应电流的有效值为$I=\frac{I_m}{{\sqrt{2}}}=\frac{2}{{\sqrt{2}}}A=\sqrt{2A}$
电压表的读数是$U=IR=\sqrt{2}×90V=90\sqrt{2}V$
(3)电动势的平均值为$\overline{E}$=$\frac{n△Φ}{△t}$
由闭合电路的欧姆定律,可得电流的平均值为$\overline I=\frac{\overline E}{R+r}$
通过电阻的电量$q=\overline I△t=\frac{nBS}{R+r}=\frac{{100×2.0×{{10}^{-2}}}}{90+10}C=2.0×{10^{-2}}C$
答:(1)交流发电机产生的电动势的最大值为200V;
(2)电路中交流电压表的示数为90$\sqrt{2}$V;
(3)线圈从图示位置开始转动90°的过程中通过电阻R的电量为2.0×10-2C.
点评 解决本题的关键知道正弦式交流电峰值的表达式Em=nBSω,以及知道峰值与有效值的关系,求解电表示数及功率时用有效值,求解电量时要用平均值.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 介质中各质点由近及远地传播开去 | |
| B. | 介质中质点的振动速度就是波传播的速度 | |
| C. | 介质点振动的能量由近及远传播开去 | |
| D. | 介质质点既有振动又有迁移 |
| A. | 核反应方程为${\;}_{2}^{3}$He+${\;}_{1}^{2}$H→${\;}_{2}^{4}$He+${\;}_{1}^{1}$H | |
| B. | 核反应生成物的质量将大于参加反应物质的质量 | |
| C. | “氦3(${\;}_{2}^{3}$He)”一个核子的结合能大于“氦 4(${\;}_{2}^{4}$He)”一个核子的结合能 | |
| D. | “氦 3(${\;}_{2}^{3}$He)”的原子核与一个氘核发生聚变将放出能量 |

 如图所示,在半径为R的水平圆盘的正上方高h处水平抛出一个小球,圆盘做匀速转动,当圆盘半径OB转到与小球水平初速度方向平行时,小球开始抛出,要使小球恰好落在B点,求小球的初速度v和圆盘转动的角速度ω.
如图所示,在半径为R的水平圆盘的正上方高h处水平抛出一个小球,圆盘做匀速转动,当圆盘半径OB转到与小球水平初速度方向平行时,小球开始抛出,要使小球恰好落在B点,求小球的初速度v和圆盘转动的角速度ω.

 在《探究求合力的方法》的实验中,
在《探究求合力的方法》的实验中,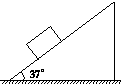 如图所示,在倾角为37°的固定斜面上,放置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8.已知sin37°=0.6,cos37°=0.8,g=10m/s2.
如图所示,在倾角为37°的固定斜面上,放置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8.已知sin37°=0.6,cos37°=0.8,g=10m/s2.