��Ŀ����
��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3
�ij��ٶ���A�㿪ʼ��B�㻬�У�AB=5R�������Ϲ⻬�İ뾶ΪR��1/4Բ��BC����C�����Ϸ���һ��C��߶�ҲΪR����תƽ̨����ƽֱ̨�����������������ľ�����ȵ�С��P��Q����תʱ�����ܴﵽC������Ϸ��� ��
��1������յ�B �����ٶȣ�
��2�����黬��C�㣬����С��Pʱ���ٶȣ�
��3�������鴩��P����ǡ�ܴ�Q�����£���ƽ̨ת���Ľ��ٶȦ�Ӧ����ʲô������
| gR |
��1������յ�B �����ٶȣ�
��2�����黬��C�㣬����С��Pʱ���ٶȣ�
��3�������鴩��P����ǡ�ܴ�Q�����£���ƽ̨ת���Ľ��ٶȦ�Ӧ����ʲô������

��1���軬����B��ʱ�ٶ�ΪvB���Ի�����A�㵽B��Ӧ�ö��ܶ����У�
-��mg5R=
mvB2-
mv02
��ã�vB2=8gR
vB=2
��2�������B�㿪ʼ�˶���������غ㣬�軬�鵽��P��ʱ�ٶ�Ϊvp����
mvB2=
mvp2+mg2R
��ã�vp=2
��3�����鴩��P���ٻص�ƽ̨��ʱ�䣺t=
=4
Ҫ��ʵ���������̣������㣺��t=��2n+1����
������ʽ�����ã���=
��n=0��1��2����
�𣺣�1������յ�B�����ٶ�2
��
��2�����黬��C�㣬����С��Pʱ���ٶ�vp=2
��
��3�������鴩��P����ǡ�ܴ�Q�����£���ƽ̨ת���Ľ��ٶȦ�Ӧ�����=
��n=0��1��2������
-��mg5R=
| 1 |
| 2 |
| 1 |
| 2 |
��ã�vB2=8gR
vB=2
| 2gR |
��2�������B�㿪ʼ�˶���������غ㣬�軬�鵽��P��ʱ�ٶ�Ϊvp����
| 1 |
| 2 |
| 1 |
| 2 |
��ã�vp=2
| gR |
��3�����鴩��P���ٻص�ƽ̨��ʱ�䣺t=
| 2vp |
| g |
|
Ҫ��ʵ���������̣������㣺��t=��2n+1����
������ʽ�����ã���=
| ��(2n+1) |
| 4 |
|
�𣺣�1������յ�B�����ٶ�2
| 2gR |
��2�����黬��C�㣬����С��Pʱ���ٶ�vp=2
| gR |
��3�������鴩��P����ǡ�ܴ�Q�����£���ƽ̨ת���Ľ��ٶȦ�Ӧ�����=
| ��(2n+1) |
| 4 |
|

��ϰ��ϵ�д�
�����Ŀ
 ��2011?�Ϻ�ģ�⣩��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3
��2011?�Ϻ�ģ�⣩��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3 ��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3
��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3 ��2009?�Ͳ���ģ����ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������
��2009?�Ͳ���ģ����ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������ ��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3
��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3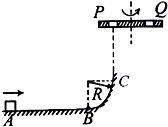 ��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3
��ͼ��ʾ����������Ϊm����ˮƽ�����Ķ�Ħ������Ϊ0.1������v0=3