题目内容
5. 如图所示,在水平面内有两根间距为L=1m的足够长的平行金属导轨ab,cd,在a,c之间用导线连接一阻值为R=3Ω的电阻,放在金属导轨ab,cd上的金属杆质量为m=0.5kg,电阻r=1Ω,与导轨间的动摩擦因数为μ=0.4,金属杆的中点系一绝缘轻细绳,细绳的另一端通过光滑的定滑轮悬挂一质量为M=1.0kg的重物,磁感应强度为B=2T的匀强磁场与导轨平面垂直,金属杆运动过程中与导轨接触良好,g取10m/s2
如图所示,在水平面内有两根间距为L=1m的足够长的平行金属导轨ab,cd,在a,c之间用导线连接一阻值为R=3Ω的电阻,放在金属导轨ab,cd上的金属杆质量为m=0.5kg,电阻r=1Ω,与导轨间的动摩擦因数为μ=0.4,金属杆的中点系一绝缘轻细绳,细绳的另一端通过光滑的定滑轮悬挂一质量为M=1.0kg的重物,磁感应强度为B=2T的匀强磁场与导轨平面垂直,金属杆运动过程中与导轨接触良好,g取10m/s2(1)将重物由静止释放,重物将开始做加速运动,若某时刻金属杆的加速度大小为a=2m/s2,求此时金属杆运动的速度大小v;
(2)重物最终将匀速下降,若M从静止到匀速的过程中下降的高度为h=8m,则在此过程中电阻R上产生的焦耳热是多少?
分析 (1)由E=BLv求出感应电动势,由欧姆定律求出电流,由安培力公式求出安培力与速度的关系式,由牛顿第二定律列式求出速度.
(2)由能量守恒定律求出R上产生的焦耳热.
解答 解:(1)金属杆的速度为v时受到的安培力为:
F=BIL=B$\frac{BLv}{R+r}$L=$\frac{{B}^{2}{L}^{2}v}{R+r}$
由牛顿第二定律得:
对M有:Mg-T=Ma
对金属杆有:T-F-μmg=ma
联立解得:v=$\frac{[Mg-(M+m)a-μmg](R+r)}{{B}^{2}{L}^{2}}$=$\frac{[10-1.5×2-0.4×5]×(3+1)}{{2}^{2}×{1}^{2}}$=5m/s
(2)重物匀速下降的过程中,根据能量守恒得:
Mgh=Q+μmgh
可得 Q=Mgh-μmgh=10×8-0.4×0.5×10=78J
故在此过程中电阻R上产生的焦耳热是 QR=$\frac{R}{R+r}$Q=$\frac{3}{3+1}$×78J=58.5J
答:
(1)此时金属杆运动的速度大小v是5m/s.
(2)在此过程中电阻R上产生的焦耳热是58.5J.
点评 该题为电磁感应与动力学综合的问题,解决本题的关键推导安培力与速度的表达式,运用隔离法研究.

练习册系列答案
相关题目
15.关于第一宇宙速度,下列说法正确的是( )
| A. | 它是人造地球卫星绕地球作匀速圆周运动的最小速度 | |
| B. | 它是人造地球卫星在圆形轨道上的最小运行速度 | |
| C. | 它是能使卫星绕地球运行的最小发射速度 | |
| D. | 它是人造卫星绕地球作椭圆轨道运行时在近地点的速度 |
16.下列叙述中正确的有( )
| A. | 伽利略最先提出了日心说 | |
| B. | 开普勒发现了行星运动的三个定律 | |
| C. | 卡文迪许发现了万有引力定律 | |
| D. | 牛顿从实验研究中发现了万有引力定律并测出了万有引力常量G |
20.做曲线运动的物体,关于其所受合力的方向,下列说法正确的是( )
| A. | 一定与该物体的速度方向垂直 | |
| B. | 一定与该物体的速度方向相同 | |
| C. | 一定与该物体的速度方向相反 | |
| D. | 一定与该物体的速度方向不在同一条直线上 |
10. 两束平行的单色光a、b射向长方形玻璃砖,光从上表面入射,恰好从下表面重叠射出,如图所示,比较两种单色光,则( )
两束平行的单色光a、b射向长方形玻璃砖,光从上表面入射,恰好从下表面重叠射出,如图所示,比较两种单色光,则( )
 两束平行的单色光a、b射向长方形玻璃砖,光从上表面入射,恰好从下表面重叠射出,如图所示,比较两种单色光,则( )
两束平行的单色光a、b射向长方形玻璃砖,光从上表面入射,恰好从下表面重叠射出,如图所示,比较两种单色光,则( )| A. | 玻璃对a光的折射率比对b光的大 | |
| B. | 在玻璃中,a光的传播速度比b光的大 | |
| C. | 在相同条件下做双缝干涉实验,a光产生的条纹间距比b光窄 | |
| D. | 将a、b光以相同的入射角从玻璃射向空气,若b光能发生全反射,则a光也一定能 |
14. 在光滑水平面上,有一块长木板,长木板左端放一个木块,木块与长木板间有摩擦,先后两次用相同的水平力F将木块拉离木板,如图所示,第1次将长木板固定,第2次长木板不固定,比较这两种情况下,相应的物理量两次相同的应是( )
在光滑水平面上,有一块长木板,长木板左端放一个木块,木块与长木板间有摩擦,先后两次用相同的水平力F将木块拉离木板,如图所示,第1次将长木板固定,第2次长木板不固定,比较这两种情况下,相应的物理量两次相同的应是( )
 在光滑水平面上,有一块长木板,长木板左端放一个木块,木块与长木板间有摩擦,先后两次用相同的水平力F将木块拉离木板,如图所示,第1次将长木板固定,第2次长木板不固定,比较这两种情况下,相应的物理量两次相同的应是( )
在光滑水平面上,有一块长木板,长木板左端放一个木块,木块与长木板间有摩擦,先后两次用相同的水平力F将木块拉离木板,如图所示,第1次将长木板固定,第2次长木板不固定,比较这两种情况下,相应的物理量两次相同的应是( )| A. | 木块受到摩擦力的大小不相同 | B. | 恒力F对木块做的功相同 | ||
| C. | 因摩擦产生的热相同 | D. | 木块获得的动能相同 |
 如图所示,水平传送带AB=5m,以v=4m/s匀速运动.一小物体与皮带间的动摩擦因数μ=0.2.
如图所示,水平传送带AB=5m,以v=4m/s匀速运动.一小物体与皮带间的动摩擦因数μ=0.2.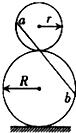 如图所示,半径分别为r和R的圆环竖直叠放(相切)于水平面上,一条公共斜弦过两圆切点且分别与两圆相交于a、b两点.在此弦上铺一条光滑轨道,将一小球从a点由静止释放,设小球穿过切点时不受阻挡.求该小球从a点运动到b点所用的时间.
如图所示,半径分别为r和R的圆环竖直叠放(相切)于水平面上,一条公共斜弦过两圆切点且分别与两圆相交于a、b两点.在此弦上铺一条光滑轨道,将一小球从a点由静止释放,设小球穿过切点时不受阻挡.求该小球从a点运动到b点所用的时间.