题目内容
18.长为L的细线,一端固定在O点,另一端系一个小球,把小球拉到与悬点O处于同一水平面的A点,并给小球竖直向下的初速度,使小球绕O点在竖直平面内做圆周运动,要使小球能够在竖直平面内做竖直圆周运动,在A处小球竖直向下的最小速度应为( )| A. | $\sqrt{3gL}$ | B. | $\sqrt{5gL}$ | C. | $\sqrt{7gL}$ | D. | $\sqrt{2gL}$ |
分析 当小球恰好通过圆周最高点B时,小球的初速度最小.根据牛顿第二定律和机械能守恒定律求出在A处小球竖直向下的最小初速度.
解答 解:当小球恰好到达圆周的最高点B时,由重力提供向心力,则有
mg=m$\frac{{v}^{2}}{L}$,得v=$\sqrt{gL}$
根据机械能守恒定律得:
mgL+$\frac{1}{2}$mv2=$\frac{1}{2}$mvA2
解得,vA=$\sqrt{3gL}$
故选:A
点评 本题是机械能守恒定律与向心力知识的综合应用.轻绳系的小球恰好到达圆周的最高点时,临界速度为v=$\sqrt{gR}$,这是圆周运动中常用的临界条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.如图所示为同轴的轻质圆盘,可以绕水平轴O转动,大轮与小轮半径之比为2:1.小轮边缘所绕的细线悬挂质量为m的物块A.大轮边缘所绕的细线与放在水平面上质量为2m的物体B相连.将物体B从距离圆盘足够远处静止释放,运动中B受到的阻力f与位移s成正比(f=ks).对于整个运动过程中,下列说法正确的是( )

| A. | 物体B先加速后减速 | |
| B. | 全程物体B克服阻力做的功等于物块A重力势能的减小量 | |
| C. | 物体B运动的最长距离为$\frac{mg}{2k}$ | |
| D. | 物体B运动的最大速度为$\frac{g}{3}$$\sqrt{\frac{m}{k}}$ |
6. 光滑绝缘水平面上固定两个等量正电荷,其连线中垂线上有A、B、C三点,如图甲所示.一个质量为m=0.1kg的小物块在水平面上由A点静止释放,小物块带正电,电荷量为q=2×10-3C,其运动的v-t图线如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列分析正确的是( )
光滑绝缘水平面上固定两个等量正电荷,其连线中垂线上有A、B、C三点,如图甲所示.一个质量为m=0.1kg的小物块在水平面上由A点静止释放,小物块带正电,电荷量为q=2×10-3C,其运动的v-t图线如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列分析正确的是( )
 光滑绝缘水平面上固定两个等量正电荷,其连线中垂线上有A、B、C三点,如图甲所示.一个质量为m=0.1kg的小物块在水平面上由A点静止释放,小物块带正电,电荷量为q=2×10-3C,其运动的v-t图线如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列分析正确的是( )
光滑绝缘水平面上固定两个等量正电荷,其连线中垂线上有A、B、C三点,如图甲所示.一个质量为m=0.1kg的小物块在水平面上由A点静止释放,小物块带正电,电荷量为q=2×10-3C,其运动的v-t图线如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列分析正确的是( )| A. | B点为中垂线上电场强度最大的点 | |
| B. | 由A点到C点,物块的电势能先增大后减小 | |
| C. | A、C两点关于B点对称 | |
| D. | 由A点到C点,电势逐渐降低 |
13. 如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )
如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )
 如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )
如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )| A. | 保持电键闭合,灵敏电流计会一直有读数 | |
| B. | 断开电键后,再将B线圈靠近A线圈的过程中,灵敏电流计会发生偏转 | |
| C. | 闭合电键瞬间,灵敏电流计会发生偏转 | |
| D. | 保持电键闭合,将滑动变阻器的滑片左右移动过程中,灵敏电流计不会偏转 |
3.一质点做直线运动,在第1s、第2s、第3s、第4s末的速度分别为v1=1m/s,v2=2m/s,v3=4m/s,v4=8m/s,则这个质点的运动 是( )
| A. | 匀速直线运动 | B. | 匀加速直线运动 | ||
| C. | 匀减速直线运动 | D. | 非匀变速直线运动 |
10.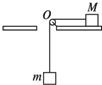 如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
 如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )| A. | 0.04 m | B. | 0.08 m | C. | 0.16 m | D. | 0.32 m |
7.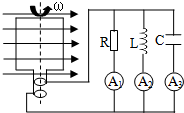 如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )
如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )
 如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )
如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )| A. | I1=2I | B. | I2=2I | C. | I3=2I | D. | I3>I1>I2 |
 如图所示,弹性小球的质量为m,钢板的质量为M(M?m),它们一起自h高处自由下落,并与弹性地板相碰,不计空气阻力,球与钢板之间的碰撞及钢板与地面之间的碰撞均为弹性碰撞,试计算钢板着地后弹性小球能够上升高度.
如图所示,弹性小球的质量为m,钢板的质量为M(M?m),它们一起自h高处自由下落,并与弹性地板相碰,不计空气阻力,球与钢板之间的碰撞及钢板与地面之间的碰撞均为弹性碰撞,试计算钢板着地后弹性小球能够上升高度.