题目内容
用质量为m、长度为L的绳沿着光滑水平面拉动质量为M的物体,在绳的一端所施加的水平拉力为F,如图所示,则物体与绳的加速度大小为 ; 绳中各处张力的大小为 .(假定绳的质量分布均匀,下垂度可忽略不计.)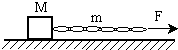
【答案】分析:(1)对物体和绳组成的整体为研究对象,根据牛顿第二定律求加速度.
(2)设绳上任一点离F作用点距离为x处绳的弹力为Tx,长为x的这段绳质量△m=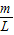 ?x,对这段绳应用牛顿第二定律求解.
?x,对这段绳应用牛顿第二定律求解.
解答:解:(1)对整体,根据牛顿第二定律,得:F=(M+m)a
∴a=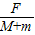
(2)设绳上任一点离F作用点距离为x处绳的弹力为Tx,则长为x的这段绳质量△m=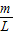 ?x
?x
对这段绳应用牛顿第二定律.
F-Tx=△ma
Tx=F-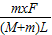
故答案为: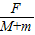 ,F-
,F-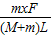 .
.
点评:应用牛顿第二定律时,首先要选择研究对象,有整体法和隔离法两种可供选择.
(2)设绳上任一点离F作用点距离为x处绳的弹力为Tx,长为x的这段绳质量△m=
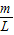 ?x,对这段绳应用牛顿第二定律求解.
?x,对这段绳应用牛顿第二定律求解.解答:解:(1)对整体,根据牛顿第二定律,得:F=(M+m)a
∴a=
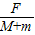
(2)设绳上任一点离F作用点距离为x处绳的弹力为Tx,则长为x的这段绳质量△m=
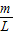 ?x
?x对这段绳应用牛顿第二定律.
F-Tx=△ma
Tx=F-
故答案为:
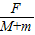 ,F-
,F-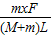 .
.点评:应用牛顿第二定律时,首先要选择研究对象,有整体法和隔离法两种可供选择.

练习册系列答案
相关题目
 用质量为m、长度为L的绳沿着光滑水平面拉动质量为M的物体,在绳的一端所施加的水平拉力为F,如图所示,则物体与绳的加速度大小为
用质量为m、长度为L的绳沿着光滑水平面拉动质量为M的物体,在绳的一端所施加的水平拉力为F,如图所示,则物体与绳的加速度大小为

