题目内容
如图所示，金属板A、金属网B、荧光屏C彼此平行，A、B之间的距离d1=9cm，B、C之间的距离d2=18cm，电源电动势E=20V，内阻r=2Ω，滑动变阻器在0～18之间可调，图中滑动片置于电阻的中点，从S孔向各个方向以速度V=1×105m/s向电场中射入电子，电子的比荷
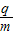=1.8×1011C/kg，不计电子重力．求（1）A、B之间的电场强度E
（2）设所有电子都能打在荧光屏上，求屏上亮圆的半径．
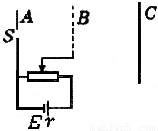
【答案】分析：（1）根据闭合电路欧姆定律，即可求解；
（2）根据运动的合成与分解，并由运动学公式与牛顿第二定律，并结合几何关系，即可求解．
解答：解：（1）设A、B两板间的电压为U，则有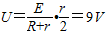
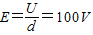
（2）对竖直向上发射的电子到达B板P点时
水平速度为：vBX=at=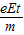
水平距离：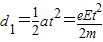
得：
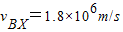
电子运动到B网竖直距离为：r1=vt=1cm
设电子到达B时，速度方向与水平方向夹角为θ，则：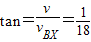
电子从B运动到C的竖直距离为：r=d2tanθ=1cm
∴屏上宽圆半径 r=r1+r2=2cm
答：（1）A、B之间的电场强度100V；
（2）设所有电子都能打在荧光屏上，则屏上亮圆的半径2cm．
点评：考查闭合电路欧姆定律、牛顿第二定律与运动学公式，掌握几何关系的应用．
（2）根据运动的合成与分解，并由运动学公式与牛顿第二定律，并结合几何关系，即可求解．
解答：解：（1）设A、B两板间的电压为U，则有
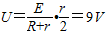
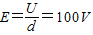
（2）对竖直向上发射的电子到达B板P点时
水平速度为：vBX=at=
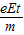
水平距离：
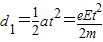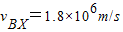
得：电子运动到B网竖直距离为：r1=vt=1cm
设电子到达B时，速度方向与水平方向夹角为θ，则：
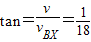
电子从B运动到C的竖直距离为：r=d2tanθ=1cm
∴屏上宽圆半径 r=r1+r2=2cm
答：（1）A、B之间的电场强度100V；
（2）设所有电子都能打在荧光屏上，则屏上亮圆的半径2cm．
点评：考查闭合电路欧姆定律、牛顿第二定律与运动学公式，掌握几何关系的应用．
练习册系列答案
相关题目
如图所示，金属板A、金属网B、荧光屏C彼此平行，A、B之间的距离d1=9cm，
如图所示，金属板A、B与电源相连，电源电压U=2V，AB板间距d=5cm，B板接地．在两板间有a、b、c三点，其连线组成一直角三角形，ab连线与A板垂直，ab长L1=3cm，a点离A板L2=1cm．
如图所示平行金属板A、B之间有匀强电场，A、B间电压为600V，A板带正电并接地，A、B两板间距为12cm，C点离A板4cm．则C点的电势为
（2004?惠州一模）如图所示，金属板A与B平行且相距为d，在A板上放置一小粒放射性物质钴60，它不断释放α粒子，这些粒子的最大速度为v，B板上涂有荧光粉．设α粒子的电量为q，质量为m，当在A、B间加电压u（uA＞uB）时，假设没有α粒子被B板反射，B板的面积足够大，试求：α粒子轰击荧光粉面使B板发光的面积为多大？