题目内容
如图示,在水平方向的匀强电场中,有一个不可伸长的绝缘细线L的一端连着质量为m带电量为q的带电小球,另一端固定于O点.现在,把小球拉起直至细线与场强平行,然后无初速释放时,发现:小球能够恰好摆到最低点B.已知本地的重力加速度为g.求:(1)该匀强电场的电场强度E的表达式;
(2)小球摆到什么位置速度最大?并导出这个最大速度的表达式.
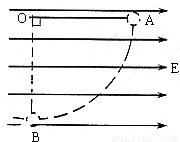
【答案】分析:对小球进行受力分析,根据共点力平衡,抓住合力等于零,运用正交分解求出拉力大小和电场力大小,从而求出电场强度.
根据动能定理求出运动到最低点的速度.
解答:解:(1)由对称性分析知,将电场与重力场合成后而形成的合场一定也是匀强场(用表示),其方向一定与AB连线的垂直平分线平行,斜指右下方方向与水平方向成45°角,电场力与重力必相等,即:mg=qE
所以,该匀强电场的电场强度E的表达式为: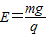
(2)根据前面的分析可知,当摆线与水平方向成45°角之时,也就是系统处于合场的“势能”最低的位置之时,也就是系统的动能处于最大的状态之时.此处,也就是摆球的速度处于最大的位置之处.
此时: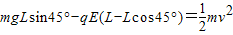
解得: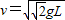
答:(1)该匀强电场的电场强度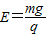 ;
;
(2)小球摆到摆线与水平方向成45°角之时什么位置速度最大,这个最大速度的表达式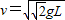 .
.
点评:本题考查了共点力平衡问题、动能定理.将电场与重力场合成后而形成的合场一定也是匀强场处关键.理是解题的捷径和
根据动能定理求出运动到最低点的速度.
解答:解:(1)由对称性分析知,将电场与重力场合成后而形成的合场一定也是匀强场(用表示),其方向一定与AB连线的垂直平分线平行,斜指右下方方向与水平方向成45°角,电场力与重力必相等,即:mg=qE
所以,该匀强电场的电场强度E的表达式为:
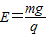
(2)根据前面的分析可知,当摆线与水平方向成45°角之时,也就是系统处于合场的“势能”最低的位置之时,也就是系统的动能处于最大的状态之时.此处,也就是摆球的速度处于最大的位置之处.
此时:
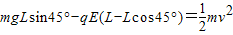
解得:
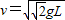
答:(1)该匀强电场的电场强度
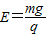 ;
;(2)小球摆到摆线与水平方向成45°角之时什么位置速度最大,这个最大速度的表达式
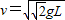 .
.点评:本题考查了共点力平衡问题、动能定理.将电场与重力场合成后而形成的合场一定也是匀强场处关键.理是解题的捷径和

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图示,在正交的匀强电场和磁场的区域内(磁场水平向内),有一离子恰能沿直线飞过此区域(不计离子重力)( )
如图示,在正交的匀强电场和磁场的区域内(磁场水平向内),有一离子恰能沿直线飞过此区域(不计离子重力)( )| A、若离子带正电,E方向应向上 | B、若离子带负电,E方向应向上 | C、若离子带正电,E方向应向下 | D、若离子带负电,E方向应向下 |
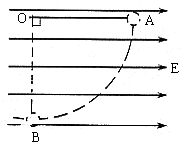 如图示,在水平方向的匀强电场中,有一个不可伸长的绝缘细线L的一端连着质量为m带电量为q的带电小球,另一端固定于O点.现在,把小球拉起直至细线与场强平行,然后无初速释放时,发现:小球能够恰好摆到最低点B.已知本地的重力加速度为g.求:
如图示,在水平方向的匀强电场中,有一个不可伸长的绝缘细线L的一端连着质量为m带电量为q的带电小球,另一端固定于O点.现在,把小球拉起直至细线与场强平行,然后无初速释放时,发现:小球能够恰好摆到最低点B.已知本地的重力加速度为g.求: 如图所示,有一矩形线圈的面积为S,匝数为N内阻不计,绕OO′轴在水平方向的磁感应强度为B的匀强磁场中以角速度ω做匀速转动,从图示位置开始计时.矩形线圈通过滑环接一理想变压器,滑动触头P上下移动时可改变输出电压,副线圈接有可调电阻R,下列判断正确的是( )
如图所示,有一矩形线圈的面积为S,匝数为N内阻不计,绕OO′轴在水平方向的磁感应强度为B的匀强磁场中以角速度ω做匀速转动,从图示位置开始计时.矩形线圈通过滑环接一理想变压器,滑动触头P上下移动时可改变输出电压,副线圈接有可调电阻R,下列判断正确的是( ) 建筑工地上的塔吊起吊重物时,在某段时间内运动轨迹如图所示,开始时重物以速度v0沿水平方向x轴运动,钢丝绳的方向始终沿竖直方向y轴.重物质量为m,若在图示的时间段内重物的水平速度和钢丝绳的拉力保持不变,今测得重物在水平方向的位移为l时,上升的高度为h,到达p位置.求:
建筑工地上的塔吊起吊重物时,在某段时间内运动轨迹如图所示,开始时重物以速度v0沿水平方向x轴运动,钢丝绳的方向始终沿竖直方向y轴.重物质量为m,若在图示的时间段内重物的水平速度和钢丝绳的拉力保持不变,今测得重物在水平方向的位移为l时,上升的高度为h,到达p位置.求: