题目内容
4.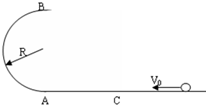 如图所示,半径R=0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.1kg的小球,以初速度v0=7m/s在水平地面上向左作加速度a=3m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,最后小球落在C点.求:
如图所示,半径R=0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.1kg的小球,以初速度v0=7m/s在水平地面上向左作加速度a=3m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,最后小球落在C点.求:(1)小球在A处的速度;
(2)小球在B处所受的支持力和速度;
(3)A、C之间的距离(g=10m/s2)
分析 要求AC之间的距离应该首先判定物体能否到达B点,故应该先求出物体到达B点的最小速度,然后根据动能定理求出物体实际到达B点时的速度,由于实际速度大于最小速度,故物体到达B后做平抛运动,最后根据平抛运动的规律求出物体在平抛过程当中水平向的位移.
解答 解:(1)小球向左运动的过程中小球做匀减速直线运动,故有:
vA2-v02=-2as
解得:vA=$\sqrt{{v}_{0}^{2}-2as}$=5m/s
(2)如果小球能够到达B点,则在B点的最小速度vmin,故有:
mg=m$\frac{{v}_{min}^{2}}{R}$
解得:vmin=2m/s
而小球从A到B的过程中根据机械能守恒可得:
mgh+$\frac{1}{2}$mvB2=$\frac{1}{2}$mvA2
解得:vB=3m/s
由于VB>vmin
故小球能够到达B点,且从B点作平抛运动,由牛顿第二定律可知:
F-mg=m$\frac{{v}_{B}^{2}}{R}$
解得:F=mg+m$\frac{{v}_{B}^{2}}{R}$=1+22.5N=23.5N;
(3)在竖直方向有:
2R=$\frac{1}{2}$gt2;
在水平方向有
sAC=vBt
解得:sAC=1.2m
故AC间的距离为1.2m;
答:(1)小球到达A点的速度为5m/s;
(2)速度大小为3m/s;
(3)AC间的距离为1.2m.
点评 解决多过程问题首先要理清物理过程,然后根据物体受力情况确定物体运动过程中所遵循的物理规律进行求解;小球能否到达最高点,这是我们必须要进行判定的,因为只有如此才能确定小球在返回地面过程中所遵循的物理规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.美国宇航员登月后,将一质量为m的物体以初速度v0水平抛出,当其竖直分位移为水平分位移的2倍时,则物体的(设月球表面的重力加速度为g)( )
| A. | 竖直分速度为水平分速度2倍 | B. | 此时重力的瞬时功率为4mgv0 | ||
| C. | 运动时间为$\frac{4{v}_{0}}{g}$ | D. | 此过程中重力做的功为4mv02 |
9.20世纪以来,人们发现了一些新的事实,而经典力学却无法解释,经典力学只适用于解决物体低速运动的问题,不能用来处理高速运动的问题;只适用于宏观物体,不适用于微观粒子.下列说法不正确的是( )
| A. | 随着认识的发展,经典力学已成了过时的理论 | |
| B. | 人们对客观事物的具体认识,在广度上是有局限性的 | |
| C. | 不同领域的事物各有其本质与规律 | |
| D. | 人们应当不断扩展认识,在更广阔的领域内掌握不同事物的本质与规律 |
 如图所示是一列简谐横波在t=0时刻的波形,已知这列波沿x轴正方向传播,波速为2m/s.P点是离原点为2m的一个介质质点,则该质点振动的周期为2s,在t=1.5s时质点P的位移为-10cm.
如图所示是一列简谐横波在t=0时刻的波形,已知这列波沿x轴正方向传播,波速为2m/s.P点是离原点为2m的一个介质质点,则该质点振动的周期为2s,在t=1.5s时质点P的位移为-10cm.
 如图所示,光滑的倾斜轨道与半径为R的圆形轨道相连接,质量为m的小球在倾斜轨道上由静止释放,要使小球恰能通过圆形轨道的最高点,求:
如图所示,光滑的倾斜轨道与半径为R的圆形轨道相连接,质量为m的小球在倾斜轨道上由静止释放,要使小球恰能通过圆形轨道的最高点,求: 如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.求:
如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.求: