题目内容
9. 如图所示,一束单色光斜射到均匀平行玻璃砖甲的上表面后,穿过其下方与之平行放置的均匀平行玻璃砖乙,光线进入甲的入射角为α,甲、乙两玻璃砖的折射率分别为n1、n2,结果光在两玻璃砖中运动的时间相等,求:两玻璃砖的厚度之比.
如图所示,一束单色光斜射到均匀平行玻璃砖甲的上表面后,穿过其下方与之平行放置的均匀平行玻璃砖乙,光线进入甲的入射角为α,甲、乙两玻璃砖的折射率分别为n1、n2,结果光在两玻璃砖中运动的时间相等,求:两玻璃砖的厚度之比.
分析 先根据折射定律求得光进入玻璃砖上表面时的折射角,由v=$\frac{c}{n}$求出光在玻璃砖内的传播速度,根据光在两玻璃砖中运动的时间相等列式,即可求解.
解答 解:设光进入甲玻璃砖的折射角为r
根据折射定律有 n1=$\frac{sinα}{sinr}$
光在玻璃砖中运动的路程 s1=$\frac{{d}_{1}}{cosr}$
运动时间 t1=$\frac{{s}_{1}}{{v}_{1}}$=$\frac{{n}_{1}{d}_{1}}{c\sqrt{1-si{n}^{2}r}}$=$\frac{{n}_{1}{d}_{1}}{c\sqrt{1-(\frac{sinα}{{n}_{1}})^{2}}}$=$\frac{{n}_{1}^{2}{d}_{1}}{c\sqrt{{n}_{1}^{2}-si{n}^{2}α}}$
根据光路可逆性可知,光在玻璃砖乙表面的入射角也为α
同理可得光在乙玻璃砖中运动的时间为 t2=$\frac{{n}_{2}^{2}{d}_{2}}{c\sqrt{{n}_{2}^{2}-si{n}^{2}α}}$
由于t1=t2,可得两玻璃砖的厚度之比为 $\frac{{d}_{1}}{{d}_{2}}$=$\frac{{n}_{2}^{2}\sqrt{{n}_{1}^{2}-si{n}^{2}α}}{{n}_{1}^{2}\sqrt{{n}_{2}^{2}-si{n}^{2}α}}$
答:两玻璃砖的厚度之比为$\frac{{n}_{2}^{2}\sqrt{{n}_{1}^{2}-si{n}^{2}α}}{{n}_{1}^{2}\sqrt{{n}_{2}^{2}-si{n}^{2}α}}$.
点评 本题是几何光学问题,运用几何知识和折射定律结合进行求解,是几何光学问题常用的方法和思路.

| A. | 改装成电压表时,串联的电阻值越大改装后的量程越大 | |
| B. | 改装成电压表时,串联的电阻值越大改装后的量程越小 | |
| C. | 改装成电流表时,并联的电阻值越大改装后的量程越大 | |
| D. | 改装成电流表时,并联的电阻值越大改装后的量程越小 |
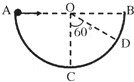 如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点.圆上有一点D,且∠COD=60°.现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点.重力加速度为g,不计空气阻力.下列说法中正确的是( )
如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点.圆上有一点D,且∠COD=60°.现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点.重力加速度为g,不计空气阻力.下列说法中正确的是( )| A. | 圆的半径为R=$\frac{4{{v}_{1}}^{2}}{3g}$ | B. | 圆的半径为R=$\frac{2{{v}_{1}}^{2}}{g}$ | ||
| C. | 甲小球能垂直击中C点 | D. | 乙小球能垂直击中D点 |
 在理想变压器原线圈a、b两端输入正弦交变电压,在调节滑片P1或P2的过程中,下列说法正确的是( )
在理想变压器原线圈a、b两端输入正弦交变电压,在调节滑片P1或P2的过程中,下列说法正确的是( )| A. | 只将P1向上移,电压表、电流表的示数都变大 | |
| B. | 只将P1向上移,电压表的示数不变,电流表的示数增大 | |
| C. | 只将P2向上移,电压表、电流表的示数都变大 | |
| D. | 只将P2向上移,电压表的示数,电流表的示数增大 |

 如图所示,A,B两轮同绕轴O转动,A和C两轮用皮带传动,A,B,C三轮的半径之比为2:3:3,a,b,c为三轮边缘上的点.求
如图所示,A,B两轮同绕轴O转动,A和C两轮用皮带传动,A,B,C三轮的半径之比为2:3:3,a,b,c为三轮边缘上的点.求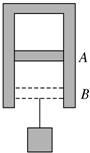 缸内壁光滑且缸壁是导热的.开始活塞静止在离气缸底部h1的A位置,在活塞下端挂上一重物后,活塞经过足够长时间后缓慢下降停在离气缸底部h2的B位置(设周围环境温度保持不变,大气压强为p0,重力加速度为g,活塞面积S),问:在该过程中,缸内气体是吸热还是放热?所挂重物的质量的多少?
缸内壁光滑且缸壁是导热的.开始活塞静止在离气缸底部h1的A位置,在活塞下端挂上一重物后,活塞经过足够长时间后缓慢下降停在离气缸底部h2的B位置(设周围环境温度保持不变,大气压强为p0,重力加速度为g,活塞面积S),问:在该过程中,缸内气体是吸热还是放热?所挂重物的质量的多少? 如图所示,空间的某一区域存在着相互垂直的匀强电场和匀强磁场,一个重力忽略的带电微粒以某一初速度由A点进入这个区域沿直线运动,从C点离开区域;如果将磁场撤去,其他条件不变,则粒子从B点离开场区;如果将电场撤去,其他条件不变,则粒子从D点离开场区.已知BC=CD,设粒子在上述三种情况下,从A到B、从A到C和从A到D所用的时间分别是t1,t2和t3,离开三点时的动能分别是Ek1、Ek2、Ek3,以下关系式正确的是( )
如图所示,空间的某一区域存在着相互垂直的匀强电场和匀强磁场,一个重力忽略的带电微粒以某一初速度由A点进入这个区域沿直线运动,从C点离开区域;如果将磁场撤去,其他条件不变,则粒子从B点离开场区;如果将电场撤去,其他条件不变,则粒子从D点离开场区.已知BC=CD,设粒子在上述三种情况下,从A到B、从A到C和从A到D所用的时间分别是t1,t2和t3,离开三点时的动能分别是Ek1、Ek2、Ek3,以下关系式正确的是( )