题目内容
15.某学校一物理课外活动小组自制了一枚火箭,火箭发射后,始终在垂直于地面的方向上运动.火箭点火后到燃料用完前做匀加速直线运动,经过4s 到达离地面40m高处时燃料恰好用完,求:(1)燃料恰好用完时火箭的速度.
(2)火箭上升离地面的最大高度.
(3)火箭从发射到残骸落向地面过程的总时间.(该大题不计空气阻力,取g=10m/s2)
分析 (1)根据平均速度公式列式求解;
(2)火箭推力消失后,由于惯性,继续上升,做上抛运动,根据速度位移公式求解继续上升的高度,最后得到总高度;
(3)燃料用完后火箭做竖直上抛运动,根据速度时间公式求出继续上升的时间,残骸落回地面过程的过程是自由落体运动,根据位移时间公式求出下落时间,总时间等于上升的总时间加上下落的时间.
解答 解:设燃料用完时火箭的速度为v1,加速度为a,所用时间为t1.火箭的运动分为两个过程,第一个过程为做匀加速上升运动,第二个过程为做竖直上抛运动至到达最高点.
(1)对第一个过程有${h}_{1}^{\;}=\frac{{v}_{1}^{\;}}{2}{t}_{1}^{\;}$
代入数据$40=\frac{{v}_{1}^{\;}}{2}×4$
解得v1=20 m/s
(2)对第二个过程有h2=$\frac{{{v}_{1}}^{2}}{2g}$
代入数据${h}_{2}^{\;}=\frac{2{0}_{\;}^{2}}{20}=20m$
所以火箭上升离地面的最大高度
h=h1+h2=40 m+20 m=60 m.
(3)从燃料用完到运动至最高点的过程中,
由v1=gt2
得t2=$\frac{v1}{g}$=$\frac{20}{10}$ s=2 s
从最高点落回地面的过程中有
h=$\frac{1}{2}$gt32,
而h=60 m,
代入数据:$60=\frac{1}{2}×10{t}_{3}^{2}$
得t3=2$\sqrt{3}$s,
故总时间t总=t1+t2+t3=(6+2$\sqrt{3}$) s.
答:答:(1)燃料恰好用完时火箭的速度为v=20m∕s;
(2)火箭上升离地面的最大高度为h=60m;
(3)火箭从发射到残骸落回地面过程的总时间为6+2$\sqrt{3}$s.
点评 本题考查了匀加速直线运动的基本公式及竖直上抛、自由落体运动的基本公式的直接应用,要注意火箭燃料耗尽后还会继续上升,最后做自由落体运动.

 如图是静电喷涂原理的示意图.喷枪喷嘴与被涂工件之间有强电场,喷嘴喷出的带电涂料微粒在强电场的作用下会向工件高速运动,最后被吸附到工件表面.则可知( )
如图是静电喷涂原理的示意图.喷枪喷嘴与被涂工件之间有强电场,喷嘴喷出的带电涂料微粒在强电场的作用下会向工件高速运动,最后被吸附到工件表面.则可知( )| A. | 微粒一定带正电 | B. | 微粒可能带正电,也可能带负电 | ||
| C. | 微粒运动过程中,电势能越来越大 | D. | 微粒运动过程中,电势能越来越小 |
| A. | 时间、弹力、加速度 | B. | 位移、重力、质量 | ||
| C. | 位移、速度、摩擦力 | D. | 时间、温度、路程 |

| A. | 卡文迪许通过扭秤实验,测出了万有引力常量 | |
| B. | 奥斯特通过实验研究,发现了电流周围存在磁场 | |
| C. | 密立根通过实验研究,测出了元电荷的数值 | |
| D. | 牛顿根据理想斜面实验,提出力不是维持物体运动的原因 |
 已知一足够长的粗糙斜面,倾角为θ,一滑块以初速度v1=16m/s从底端A点滑上斜面,经2s滑至最高点B后又返回到A点.其运动过程的v-t图象如图所示.已知上滑的加速度大小是下滑的4倍.求:(已知sin 37°=0.6,cos 37°=0.8,重力加速度g=10m/s2)
已知一足够长的粗糙斜面,倾角为θ,一滑块以初速度v1=16m/s从底端A点滑上斜面,经2s滑至最高点B后又返回到A点.其运动过程的v-t图象如图所示.已知上滑的加速度大小是下滑的4倍.求:(已知sin 37°=0.6,cos 37°=0.8,重力加速度g=10m/s2)

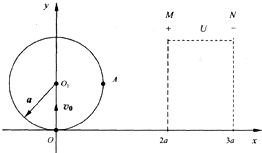 如图所示,在坐标系xOy内有一半径为d的圆形区域,圆心坐标为O1(0,a),圆内分布有垂直纸面向里的匀强磁场.在M、N之间的矩形区域(即x=2a,x=3a和y=0,y=2a所围成的区域)内有一沿+x方向的匀强电场.一质量为m、电荷量为-q(q>0)的粒子以速度v0从O点垂直于磁场沿+y轴方向射入,粒子恰好从A点射出磁场,A、O1两点的连线与x轴平行.(不计粒子重力)
如图所示,在坐标系xOy内有一半径为d的圆形区域,圆心坐标为O1(0,a),圆内分布有垂直纸面向里的匀强磁场.在M、N之间的矩形区域(即x=2a,x=3a和y=0,y=2a所围成的区域)内有一沿+x方向的匀强电场.一质量为m、电荷量为-q(q>0)的粒子以速度v0从O点垂直于磁场沿+y轴方向射入,粒子恰好从A点射出磁场,A、O1两点的连线与x轴平行.(不计粒子重力)