题目内容
20. 如图甲所示,面积为S的N匝数线圈A处在磁场中,磁场方向垂直于线圈平面,磁感应强度随时间变化的规律如图乙所示,设垂直线圈平面向外为磁场的正方向,电阻R1、R2、R3,电容C,线圈A的电阻r,B0、t0均为已知量,t=0时刻,闭合开关S.
如图甲所示,面积为S的N匝数线圈A处在磁场中,磁场方向垂直于线圈平面,磁感应强度随时间变化的规律如图乙所示,设垂直线圈平面向外为磁场的正方向,电阻R1、R2、R3,电容C,线圈A的电阻r,B0、t0均为已知量,t=0时刻,闭合开关S.(1)t=$\frac{{t}_{0}}{2}$时,求通过R2的电流大小及方向.
(2)t=t1时刻断开S,求S断开后通过R2的电荷量.
分析 (1)线圈平面垂直处于匀强磁场中,当磁感应强度随时间均匀变化时,线圈中的磁通量发生变化,从而导致出现感应电动势,由楞次定律可判断电流的方向,由法拉第电磁感应定律求出感应电动势,再利用欧姆定律求出感应电流.
(2)通过电阻R2的电量就是电容器的电量.
解答 解:(1)根据法拉第电磁感应定律有:$E=N\frac{{B}_{0}^{\;}}{{t}_{0}^{\;}}S$
根据闭合电路欧姆定律,有$I=\frac{E}{{R}_{1}^{\;}+{R}_{2}^{\;}+r}$
所以$I=\frac{N{B}_{0}^{\;}S}{{t}_{0}^{\;}({R}_{1}^{\;}+{R}_{2}^{\;}+r)}$
根据楞次定律知,通过${R}_{2}^{\;}$的电流方向由a到b
(2)S断开后,则通过${R}_{2}^{\;}$的电荷量为S断开前电容器C所带的电荷量
$q=CI{R}_{2}^{\;}$
解得:$q=\frac{CN{B}_{0}^{\;}S{R}_{2}^{\;}}{{t}_{0}^{\;}({R}_{1}^{\;}+{R}_{2}^{\;}+r)}$
答:(1)t=$\frac{{t}_{0}}{2}$时,通过R2的电流大小$\frac{N{B}_{0}^{\;}S}{{t}_{0}^{\;}({R}_{1}^{\;}+{R}_{2}^{\;}+r)}$,方向由a到b.
(2)t=t1时刻断开S,S断开后通过R2的电荷量为$\frac{CN{B}_{0}^{\;}S{R}_{2}^{\;}}{{t}_{0}^{\;}({R}_{1}^{\;}+{R}_{2}^{\;}+r)}$
点评 考查楞次定律来判定感应电流方向,由法拉第电磁感应定律来求出感应电动势大小.当然本题还注意与电路知识的结合和求解方法是解题的核心.

 如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,可视为不变.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时,下列说法正确的是( )
如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,可视为不变.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时,下列说法正确的是( )| A. | 变压器的输入功率在增大 | B. | A1表的示数和A2 表的示数均增大 | ||
| C. | V1表的示数和V2表的示数均增大 | D. | 变压器的输入功率在减小 |
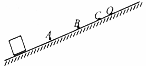 如图所示,在粗糙斜面上有一个质量为m的小物体,某时刻给它一个初速度,使其沿斜面向上做匀减速直线运动,依次经过A、B、C三点后停在O点,A、B、C三点到O点的距离分别为L1、L2、L3,为小物块由A、B、C三点运动到O点所用的时间分别为t1、t2、t3,则下列结论正确的是( )
如图所示,在粗糙斜面上有一个质量为m的小物体,某时刻给它一个初速度,使其沿斜面向上做匀减速直线运动,依次经过A、B、C三点后停在O点,A、B、C三点到O点的距离分别为L1、L2、L3,为小物块由A、B、C三点运动到O点所用的时间分别为t1、t2、t3,则下列结论正确的是( )| A. | $\frac{{L}_{1}}{{t}_{1}}$=$\frac{{L}_{2}}{{t}_{2}}$=$\frac{{L}_{3}}{{t}_{3}}$ | B. | $\frac{{L}_{1}}{{t}_{1}^{2}}$=$\frac{{L}_{2}}{{t}_{2}^{2}}$=$\frac{{L}_{3}}{{t}_{3}^{2}}$ | ||
| C. | $\frac{{L}_{1}}{{t}_{1}}$<$\frac{{L}_{2}}{{t}_{2}}$<$\frac{{L}_{3}}{{t}_{3}}$ | D. | $\frac{{L}_{1}}{{t}_{1}^{2}}$<$\frac{{L}_{2}}{{t}_{2}^{2}}$<$\frac{{L}_{3}}{{t}_{3}^{2}}$ |
| A. | 电场线越密的地方,电势越高 | |
| B. | 逆着电场线的方向电势逐渐升高 | |
| C. | 电势为零的地方,电场强度也一定为零 | |
| D. | 检验电荷沿等势面移动时,不受电场力的作用 |
 甲乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图中,直线a、b分别描述了甲乙两车在0~20s的运动情况.在这段过程中关于两车之间的位置关系,下列说法正确的是( )
甲乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图中,直线a、b分别描述了甲乙两车在0~20s的运动情况.在这段过程中关于两车之间的位置关系,下列说法正确的是( )| A. | 在0~10 s内两车逐渐靠近,10s时两车距离最近 | |
| B. | 在0~10 s内两车逐渐远离,10s时两车距离最远 | |
| C. | 在5~15 s时间段两车的位移相等,15s时两车相遇 | |
| D. | 在10~20 s内甲车始终在乙车前面,直至20s时两车相遇 |
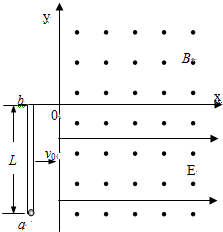 在一足够大的光滑水平面上建立如图所示的xoy坐标系,第一、四象限存在方向竖直向上、磁感应强度为B的匀强磁场;第四象限存在沿x轴正方向、电场强度为E的匀强电场.一长为L内壁光滑的薄玻璃管与y轴平行放置在水平面上的第三象限,开口端b与x轴重合,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管带着小球以水平速度v0沿x轴正方向运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从y轴飞离磁场.设运动过程中小球的电荷量保持不变,求:
在一足够大的光滑水平面上建立如图所示的xoy坐标系,第一、四象限存在方向竖直向上、磁感应强度为B的匀强磁场;第四象限存在沿x轴正方向、电场强度为E的匀强电场.一长为L内壁光滑的薄玻璃管与y轴平行放置在水平面上的第三象限,开口端b与x轴重合,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管带着小球以水平速度v0沿x轴正方向运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从y轴飞离磁场.设运动过程中小球的电荷量保持不变,求: 如图所示,理想变压器的原线圈与一矩形导轨相连,导轨间距l=10cm,导轨间有磁感应强度B=50$\sqrt{2}$T/s的匀强磁场,一金属杆紧贴导轨垂直放置.已知闭合铁芯上的三个线圈匝数n1=100匝,n2=50匝,n3=10匝,灯泡电阻RL1=10Ω,RL2=2Ω.现金属杆在外力的作用下以随时间变化规律为v=4cos100πt m/s的速度沿导轨做切割磁感线运动.请求出图中电压表和电流表的读数.
如图所示,理想变压器的原线圈与一矩形导轨相连,导轨间距l=10cm,导轨间有磁感应强度B=50$\sqrt{2}$T/s的匀强磁场,一金属杆紧贴导轨垂直放置.已知闭合铁芯上的三个线圈匝数n1=100匝,n2=50匝,n3=10匝,灯泡电阻RL1=10Ω,RL2=2Ω.现金属杆在外力的作用下以随时间变化规律为v=4cos100πt m/s的速度沿导轨做切割磁感线运动.请求出图中电压表和电流表的读数.