题目内容
12. 如图,物块a、b和c的质量相同,a和b之间用轻弹簧S相连,通过1、2两根完全相同的轻绳系着悬挂于固定点O;整个系统处于静止状态;现将轻绳或轻弹簧剪断,将物块a的加速度记为a1,物块b的加速度记为a2,物块c的加速度记为a3,重力加速度大小为g,在剪断瞬间( )
如图,物块a、b和c的质量相同,a和b之间用轻弹簧S相连,通过1、2两根完全相同的轻绳系着悬挂于固定点O;整个系统处于静止状态;现将轻绳或轻弹簧剪断,将物块a的加速度记为a1,物块b的加速度记为a2,物块c的加速度记为a3,重力加速度大小为g,在剪断瞬间( )| A. | 剪断轻绳1时,a1=3g a2=0 a3=0 | B. | 剪断轻绳1时,a1=3g a2=g a3=g | ||
| C. | 剪断轻绳2时,a1=0 a2=g a3=g | D. | 剪断弹簧S时,a1=0 a2=0 a3=0 |
分析 对细线剪短前后的a、b、c物体分别受力分析,然后根据牛顿第二定律求解加速度与弹簧的伸长量.
解答 解:开始时a、b、c都处于平衡状态,对整体进行受力分析可知,整体受到重力和绳子1 的拉力,由二力平衡可知,绳子1 的拉力是T=3mg;
对b和c组成的整体进行受力分析可知,b与c的整体受到重力和弹簧的拉力,由二力平衡可知,弹簧的拉力是F=2mg;
对c进行受力分析可知,c受到重力和绳子2的拉力,根据二力平衡可知 绳子2的拉力T′等于mg.
A、B、剪断轻绳1时,a的一瞬间的位置不变,所以弹簧的拉力不变,a受到重力和弹簧的拉力,则:ma1=mg+F=mg+2mg=3mg.所以:a1=3g;
以b与c组成的整体为研究对象,则整体仍然受到重力和弹簧的拉力,重力不变,弹簧的拉力与没有变化,所以整体受到的合外力仍然等于0,所以b与c的加速度都是0.故A正确,B错误;
C、剪断轻绳2时,物体c只受到重力的作用,所以:a3=g;
剪断轻绳2时的瞬间,b的位置没有变化,所以弹簧的拉力不变,所以b受到重力和弹簧的拉力,则:
ma2=mg-F=mg-2mg=-mg,所以:a2=-g,负号表示方向向上.
c仍然受到重力和弹簧的拉力F,则:ma1=mg+F-T=mg+2mg-3mg=0
所以:a1=0.故C错误;
D、剪断弹簧S时,弹簧的弹力变成0,此时拉力a的绳子的拉力可以发生突变,a仍然处于静止状态,所以a1=0;弹簧的弹力变成0,此时拉力a的绳子的拉力可以发生突变;
以b与c为整体可知,它们只受到重力的作用,所以整体的加速度等于g.此时绳子2d的拉力变成0.所以可知:a2=g; a3=g.故D错误.
故选:A
点评 考查了牛顿第二定律的瞬时性的应用,重点区分绳和弹簧弹力的特点,注意弹簧的弹力不能突变,因形变需要过程,绳的弹力可以突变,同时要注意加速度与受力的瞬时对应关系.

| A. | 某段时间内的平均速度等于这段时间内的初速度和末速度之和的一半 | |
| B. | 在任意相等的时间内位移的变化相等 | |
| C. | 在任意相等的时间内速度的变化相等 | |
| D. | 一段时间内的平均速度,等于这段时间中点的瞬时速度 |
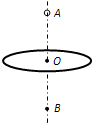 如图所示,一固定的水平玻璃均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.先将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度v0,重力加速度为g,则下列判断正确的是( )
如图所示,一固定的水平玻璃均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.先将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度v0,重力加速度为g,则下列判断正确的是( )| A. | 带电圆环在B点产生的场强方向竖直向上 | |
| B. | 小球从A点运动到B点的过程中带电小球的电势能一直增大 | |
| C. | 小球从A点运动到B点的过程中通过O点时速度最大 | |
| D. | 小球通过B点时的速度大小为$\sqrt{{{v}_{0}}^{2}+4gh}$ |

(1)实验中为了使钩码和小盘的总重力可以代替小车所受合外力,则ABC(填序号).
A.必须先平衡小车与木板之间的摩擦力
B.必须使拉小车的细线与板面平行
C.必须使小车的质量远大于钩码和小盘的总质量
D.必须先接通打点计时器的电源,再释放纸带
(2)图乙为该同学某次实验得到的纸带,根据纸带可求出小车的加速度大小为4.8m/s.也可以求出打点计时器打下D点时小车的速度为2.0m/s.(结果均保留2位有效数字)
(3)下表为该同学在保持钩码和小盘质量不变、改变小车质量m时,分别得到的小车加速度a与质量m的数据:
| 实验次数 | l | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 小车加速度a/m•s-2 | 1.98 | 1.72 | 1.48 | l.25 | 1.00 | 0.75 | 0.48 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 0.75 | 1.00 | 1.67 |
 如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点的电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子在仅受电场力的作用下开始运动,则以下说法正确的是( )
如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点的电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子在仅受电场力的作用下开始运动,则以下说法正确的是( )| A. | 电子将沿x正方向运动 | B. | 电子的电势能将变大 | ||
| C. | 电子运动的加速度先增大后减小 | D. | 电子运动的加速度一直增大 |
 如图所示,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度a1、a2,重力加速度大小为g,则有( )
如图所示,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度a1、a2,重力加速度大小为g,则有( )| A. | a1=0 a2=g | B. | a1=g a2=g | C. | a1=0 a2=$\frac{m+M}{M}$g | D. | a1=g a2=$\frac{m+M}{M}$g |

 如图所示,一倾角θ=37°的斜面上叠放着质量均为m的木板和物块,木板上表面光滑,下表面与斜面间的动摩擦因数为0.5,开始时让它们均静止,某时刻释放,则下列图象中能正确反映木板运动情况的是(tan37°=$\frac{3}{4}$)( )
如图所示,一倾角θ=37°的斜面上叠放着质量均为m的木板和物块,木板上表面光滑,下表面与斜面间的动摩擦因数为0.5,开始时让它们均静止,某时刻释放,则下列图象中能正确反映木板运动情况的是(tan37°=$\frac{3}{4}$)( )



