��Ŀ����
 ��ͼ��ʾ��ƽ�еĹ⻬�������죬���ΪL��λ��ͬһ��ֱƽ���ڣ����������е���R�����ʽ�����ab��Ϊ2L������������ֱ���ã���b��ΪL/2���̶�������Ϊm��������װ�ô��ڴŸ�Ӧǿ��ΪB����ֱ�ڵ���ƽ�����ǿ�ų��У���ab���ɾ�ֹ��ʼ����������b���������ɵ�����ˮƽλ��ʱ������ٶ�Ϊv���������㹻�������켰�����˵��費�ƣ�����˹����У�
��ͼ��ʾ��ƽ�еĹ⻬�������죬���ΪL��λ��ͬһ��ֱƽ���ڣ����������е���R�����ʽ�����ab��Ϊ2L������������ֱ���ã���b��ΪL/2���̶�������Ϊm��������װ�ô��ڴŸ�Ӧǿ��ΪB����ֱ�ڵ���ƽ�����ǿ�ų��У���ab���ɾ�ֹ��ʼ����������b���������ɵ�����ˮƽλ��ʱ������ٶ�Ϊv���������㹻�������켰�����˵��費�ƣ�����˹����У���1������R���ĵĵ��ܣ�
��2��R�еĵ������ֵ��
��������1����ab������ֱ����ת����ˮƽλ�õĹ����У�С��Ļ�е�ܼ�Сת��Ϊ���ܣ����������غ㶨��������R���ĵĵ��ܣ�
��2����ab��Ҫ����EFʱ���и��ٶ�������ĸ�Ӧ���������ab����EF��ab�ﵽˮƽλ�õĹ����У��ɻ�е���غ���ʽ���ab��Ҫ����EFʱС����ٶȣ��ɷ����ڵ�Ÿ�Ӧ���ɺ�ŷķ���ɽ�����ĵ��������ֵ��
��2����ab��Ҫ����EFʱ���и��ٶ�������ĸ�Ӧ���������ab����EF��ab�ﵽˮƽλ�õĹ����У��ɻ�е���غ���ʽ���ab��Ҫ����EFʱС����ٶȣ��ɷ����ڵ�Ÿ�Ӧ���ɺ�ŷķ���ɽ�����ĵ��������ֵ��
����⣺��1����ab������ֱ����ת����ˮƽλ�õĹ����У��������غ�
mg
=
mv2+��E��
�õ���R���ĵĵ��ܡ�E��=mg
-
mv2
��2����ab��Ҫ����EFʱ�����������������
I=
=
����
abΪ��Ҫ����EFʱab����ƽ���ٶȣ�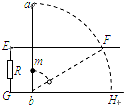
��ab����EF��ab�ﵽˮƽλ�õĹ����У��ɻ�е���غ�
mg?
+
mv
=
mv2
��v��=
ab
�������� I=2BL
��
��1������R���ĵĵ���Ϊmg
-
mv2��
��2��R�еĵ������ֵ��2BL
��
mg
| L |
| 2 |
| 1 |
| 2 |
�õ���R���ĵĵ��ܡ�E��=mg
| L |
| 2 |
| 1 |
| 2 |
��2����ab��Ҫ����EFʱ�����������������
I=
| E |
| R |
B?2L?
| ||
| R |
����
. |
| v |

��ab����EF��ab�ﵽˮƽλ�õĹ����У��ɻ�е���غ�
mg?
| L |
| 4 |
| 1 |
| 2 |
2 �� |
| 1 |
| 2 |
��v��=
| 1 |
| 2 |
. |
| v |
�������� I=2BL
4v2-
|
��
��1������R���ĵĵ���Ϊmg
| L |
| 2 |
| 1 |
| 2 |
��2��R�еĵ������ֵ��2BL
4v2-
|
����������ת���и�Ÿ��ߵ����ͣ���Ӧ�綯�ƹ�ʽE=BLv��v�Ǹ��е�����ٶȴ�С�����������غ㶨��������ǹ��õ�˼·��

��ϰ��ϵ�д�
 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
�����Ŀ
 ��2013?��̨��ģ������ͼ��ʾ���Ϊ�ȵĹ⻬б���ϣ������������Ÿ�Ӧǿ�ȴ�С��ΪB����ǿ�ų�������I�Ĵų�����ֱб�����ϣ������Ĵų�����ֱб�����£��ų��Ŀ��Ⱦ�ΪL��һ����Ϊm������ΪR���߳�Ϊ
��2013?��̨��ģ������ͼ��ʾ���Ϊ�ȵĹ⻬б���ϣ������������Ÿ�Ӧǿ�ȴ�С��ΪB����ǿ�ų�������I�Ĵų�����ֱб�����ϣ������Ĵų�����ֱб�����£��ų��Ŀ��Ⱦ�ΪL��һ����Ϊm������ΪR���߳�Ϊ

