题目内容

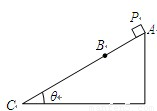
如图所示，固定斜面倾角为θ，整个斜面分为AB、BC两段，且2AB＝BC.小物块P（可视为质点）与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放，恰好能滑动到C点而停下，那么θ、μ1、μ2间应满足的关系是

A．tanθ＝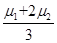

B．tanθ＝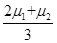

C．tanθ＝2μ1－μ2

D．tanθ＝2μ2－μ1

 

【答案】

A

【解析】

试题分析：设AB长度为s,全程根据动能定理，有：

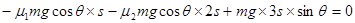
解得：tanθ＝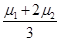

故选A

考点：本题考查对动能定理的应用，

点评：在应用动能定理的解题步骤是：进行受力分析、运动过程的分析、力的做功情况，确定初末状态，应用动能定理列公式求解，注意不要丢掉重力做功

 

练习册系列答案
相关题目
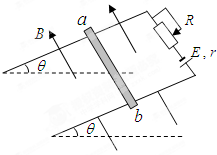
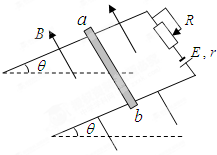如图所示，在倾θ=30°的绝缘斜面上，固定一L=0.25m的平行金属导轨，在导轨上端接入电源和滑动变阻器，电源电动E=12V，内r=1Ω，一质m=20g的金属ab与两导轨垂直并接触良好，整个装置处于磁感应强B=0.8T，方向垂直于斜面向上的匀强磁场中．金属导轨光滑，导轨与金属棒的电阻不计，g=10m/s2，要保持金属棒在导轨上静止，求：
（1）请画出金属棒受力分析图并计算通过金属棒的电流．
（2）滑动变阻器R接入电路中的阻值．
如图所示，两个质量相等而粗糙程度不同的物体m1和m2，分别固定在一细棒的两端，放在一倾角为α的斜面上，设m1和m2与斜面的摩擦因数为μ1和μ2，并满足tanα=
μ1μ2
，细棒的质量不计，与斜面不接触，试求两物体同时有最大静摩擦力时棒与斜面上最大倾斜线AB的夹角θ的余弦值（最大静摩擦力依据滑动摩擦力公式计算）
如图所示，编号1是倾角为37°的三角形劈，编号2、3、4、5、6是梯形劈，三角形劈和梯形劈斜面部分位于同一倾斜面内，构成一个完整的斜面体，可视为质点的物块m质量为1kg，与斜面部分的动摩擦因数均为μ1=0.5，三角形劈和梯形劈的质量M=1kg，劈的斜面长度均为l=0.3m，与地面的动摩擦因数均为μ2=0.2，他们紧靠在水平面上，现使物块以平行于斜面方向的速度v=6m/s从三角形劈的低端冲上斜面，假定最大静摩擦等于滑动摩擦，问：
精英家教网
（1）若是所有劈都固定在平面上，通过计算判断物块能否从第六块劈的右上端飞出；
（2）若斜面不固定，物块滑动到第几块劈时，梯形劈开始相对地面滑动？
（3）劈开始相对地面滑动时，物块的速度是多少？
如图所示，在倾θ=30°的绝缘斜面上，固定一L=0.25m的平行金属导轨，在导轨上端接入电源和滑动变阻器，电源电动E=12V，内r=1Ω，一质m=20g的金属ab与两导轨垂直并接触良好，整个装置处于磁感应强B=0.8T，方向垂直于斜面向上的匀强磁场中．金属导轨光滑，导轨与金属棒的电阻不计，g=10m/s2，要保持金属棒在导轨上静止，求：
（1）请画出金属棒受力分析图并计算通过金属棒的电流．
（2）滑动变阻器R接入电路中的阻值．
精英家教网
如图所示，在倾θ=30°的绝缘斜面上，固定一L=0.25m的平行金属导轨，在导轨上端接入电源和滑动变阻器，电源电动E=12V，内r=1Ω，一质m=20g的金属ab与两导轨垂直并接触良好，整个装置处于磁感应强B=0.8T，方向垂直于斜面向上的匀强磁场中．金属导轨光滑，导轨与金属棒的电阻不计，g=10m/s2，要保持金属棒在导轨上静止，求：
（1）请画出金属棒受力分析图并计算通过金属棒的电流．
（2）滑动变阻器R接入电路中的阻值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网