题目内容
(2009?南京一模)如图所示,光滑绝缘斜面的倾角为θ,斜面上放置一质量为M,电阻为R、边长为L的正方形导线框abcd,通过细线绕过光滑的定滑轮与一质量为m的重物相连,连接线框的细线与线框共面,滑轮和绳的质量均不计.斜面上有两个匀强磁场区域I和Ⅱ,其宽度均为L,磁感应强度大小均为B,磁场方向分别垂直于斜面向上和垂直于斜面向下线框的ab边距磁场区域I的上边界为2L开始时各段绳都处于伸直状态,现将它们由静止释放.线框沿斜面向下运动,ab边刚穿过两磁场的分界线OO'进入磁场区域Ⅱ时,线框恰好做匀速运动(绳子始终处于拉紧状态)求:
(1)线框的ab边刚进入磁场区域I时的速度大小;
(2)线框ab边在磁场区域Ⅱ中运动的过程中.线框重力的功率P;
(3)从开始释放到ab边刚穿出磁场区域I的过程中,线框中产生的焦耳热Q

(1)线框的ab边刚进入磁场区域I时的速度大小;
(2)线框ab边在磁场区域Ⅱ中运动的过程中.线框重力的功率P;
(3)从开始释放到ab边刚穿出磁场区域I的过程中,线框中产生的焦耳热Q

分析:(1)在ab边进入磁场前,线框和重物组成的系统机械能守恒,由机械能守恒定律列式求ab边刚进入磁场区域I时的速度大小;
(2)线框ab边在磁场区域Ⅱ中运动的过程中.线框重力的功率P=Mgsinθ?v2.根据法拉第定律、欧姆定律、安培力公式和平衡条件列式,求得线框在区域Ⅱ中运动的速度,即可求解.
(3)从开始释放到ab边刚穿出磁场区域I的过程中,全过程中,系统的机械能减小转化为热量,根据能量守恒列式求热量.
(2)线框ab边在磁场区域Ⅱ中运动的过程中.线框重力的功率P=Mgsinθ?v2.根据法拉第定律、欧姆定律、安培力公式和平衡条件列式,求得线框在区域Ⅱ中运动的速度,即可求解.
(3)从开始释放到ab边刚穿出磁场区域I的过程中,全过程中,系统的机械能减小转化为热量,根据能量守恒列式求热量.
解答:解:(1)对线框和重物利用机械守恒定律有:2MgLsinθ-2mgL=
(M+m)
①
解得:υ1=
②
(2)设线框ab边刚进入磁场Ⅱ时速度为v2,则线框中产生的电流为:I=
③
线框受到的安培力:F=2BIL=
④
设绳对线框、m的拉力大小为T则;
对线框;T+F=Mgsinθ ⑤
对m;T=mg ⑥
联立④⑤⑥解得:υ2=
⑦
P=Mg?sinθ?υ2=
⑧
(3)从线框开始释放到ab边刚穿出磁场Ⅱ的过程中,根据能量守恒有:4MgLsinθ-4mgL=Q+
(M+m)
⑨
联立⑦⑨得:Q=4(Msinθ-m)gL-
(M+m)[
]2⑩
答:
(1)线框的ab边刚进入磁场区域I时的速度大小为
;
(2)线框ab边在磁场区域Ⅱ中运动的过程中,线框重力的功率P为
;
(3)从开始释放到ab边刚穿出磁场区域I的过程中,线框中产生的焦耳热Q为4(Msinθ-m)gL-
(M+m)[
]2
| 1 |
| 2 |
| υ | 2 1 |
解得:υ1=
|
(2)设线框ab边刚进入磁场Ⅱ时速度为v2,则线框中产生的电流为:I=
| 2BLυ2 |
| R |
线框受到的安培力:F=2BIL=
| 4B2L2v2 |
| R |
设绳对线框、m的拉力大小为T则;
对线框;T+F=Mgsinθ ⑤
对m;T=mg ⑥
联立④⑤⑥解得:υ2=
| (Msinθ-m)gR |
| 4B2L2 |
P=Mg?sinθ?υ2=
| M(Msinθ-m)g2Rsinθ |
| 4B2L2 |
(3)从线框开始释放到ab边刚穿出磁场Ⅱ的过程中,根据能量守恒有:4MgLsinθ-4mgL=Q+
| 1 |
| 2 |
| υ | 2 2 |
联立⑦⑨得:Q=4(Msinθ-m)gL-
| 1 |
| 2 |
| (Msinθ-m)gR |
| 4B2L2 |
答:
(1)线框的ab边刚进入磁场区域I时的速度大小为
|
(2)线框ab边在磁场区域Ⅱ中运动的过程中,线框重力的功率P为
| M(Msinθ-m)g2Rsinθ |
| 4B2L2 |
(3)从开始释放到ab边刚穿出磁场区域I的过程中,线框中产生的焦耳热Q为4(Msinθ-m)gL-
| 1 |
| 2 |
| (Msinθ-m)gR |
| 4B2L2 |
点评:本题是电磁感应中的力学问题,安培力的计算和分析能量如何转化是解题关键,要加强训练,熟练掌握法拉第定律、欧姆定律、安培力等等基础知识,提高解题能力.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 (2009?南京一模)如图所示,足够长的木板质量M=10kg,放置于光滑水平地面上,以初速度v0=5m/s沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时,将一小铁块贴着挡板无初速度地放在木板上,小铁块与木板的上表面间的动摩擦因数μ=0.5,当木板运动了L=1m时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块.只要木板运动了L就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=10m/s2)试问:
(2009?南京一模)如图所示,足够长的木板质量M=10kg,放置于光滑水平地面上,以初速度v0=5m/s沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时,将一小铁块贴着挡板无初速度地放在木板上,小铁块与木板的上表面间的动摩擦因数μ=0.5,当木板运动了L=1m时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块.只要木板运动了L就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=10m/s2)试问: (2009?南京一模)如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( )
(2009?南京一模)如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( ) (2009?南京一模)用电高峰期,电灯往往会变碚,其原理可简化为如下问题如图所示,理想变压器的副线圈上,通过输电线连接两只灯泡L1和L2,输电线的等效电阻为R,原线圈输入恒定的交变电压.开始时,开关S断开,当开关S闭合时,以下说法正确的有( )
(2009?南京一模)用电高峰期,电灯往往会变碚,其原理可简化为如下问题如图所示,理想变压器的副线圈上,通过输电线连接两只灯泡L1和L2,输电线的等效电阻为R,原线圈输入恒定的交变电压.开始时,开关S断开,当开关S闭合时,以下说法正确的有( )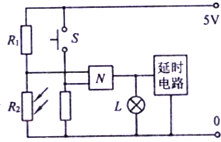 (2009?南京一模)如图所示是一个由声控开关S、光敏电阻R2、小灯泡L等元件构成的自动控制电路,该电路常用于控制居民小区里的楼道灯.白天,即使拍手发出声音,楼道灯也不会亮;到了晚上,只要拍手发出声音,灯就会亮,并采用延时电路,使之亮一段时间后才熄灭.对此电路下面说法正确的有:( )
(2009?南京一模)如图所示是一个由声控开关S、光敏电阻R2、小灯泡L等元件构成的自动控制电路,该电路常用于控制居民小区里的楼道灯.白天,即使拍手发出声音,楼道灯也不会亮;到了晚上,只要拍手发出声音,灯就会亮,并采用延时电路,使之亮一段时间后才熄灭.对此电路下面说法正确的有:( )