题目内容
14. 如图所示,坐标平面的第Ⅰ象限内存在电场强度大小为E,方向水平向左的匀强电场,第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.足够长的挡板MN垂直x轴放置,且距原点O的距离为d.若一质量为m、带电荷量为-q的粒子(不计重力)自距原点O为L的A点第一次以大小为v0,方向沿y轴正方向的速度进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点第二次进入磁场,但初速度大小为2$\sqrt{2}$v0,为使粒子进入电场后能垂直打在挡板上,求:
如图所示,坐标平面的第Ⅰ象限内存在电场强度大小为E,方向水平向左的匀强电场,第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.足够长的挡板MN垂直x轴放置,且距原点O的距离为d.若一质量为m、带电荷量为-q的粒子(不计重力)自距原点O为L的A点第一次以大小为v0,方向沿y轴正方向的速度进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点第二次进入磁场,但初速度大小为2$\sqrt{2}$v0,为使粒子进入电场后能垂直打在挡板上,求:(1)粒子在A点第二次进入磁场时,其速度方向与x轴正方向之间的夹角.
(2)粒子在A点第二次进入磁场时,该粒子到达挡板上时的速度大小及打到挡板MN上的位置到x轴的距离.
分析 以v0进入时半经为$\frac{1}{2}$L为参考条件,求得以2$\sqrt{2}$v0进入时的半径,并由垂直进入电场确定出圆心在Y轴上,画出运动轨迹图,以求得夹角;确定具体运动过程后,可由动能定理求得距离.
解答 解:(1)设速度为v0时进入磁场后做圆周运动的半径为r,
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{r}$,解得:r=$\frac{m{v}_{0}}{qB}$=$\frac{1}{2}$L,
设速度为2$\sqrt{2}$v0时进入磁场做圆周运动的半径r′,
由牛顿第二定律得:q•2$\sqrt{2}$v0B=m$\frac{(2\sqrt{2}{v}_{0})^{2}}{r′}$,解得:r=$\sqrt{2}$L,
设其速度方向与x轴正方向之间的夹角为θ,
由图中的几何关系有:cosθ=$\frac{L}{r′}$=$\frac{\sqrt{2}}{2}$,解得:θ=45°或θ=135°;
(2)为使粒子进入电场后能垂直打在挡板上,
要求粒子进入电场时速度方向与x轴正方向平行,如图所示.
粒子进入电场后,由动能定理有:qEd=$\frac{1}{2}$mv′2-$\frac{1}{2}$m(2$\sqrt{2}$v0)2,
解得:v′=$\sqrt{8{v}_{0}^{2}+\frac{2qEd}{m}}$,
当θ1=45°时,粒子打到挡板MN上的位置到x轴的距离为:
y1=r′-r′sin45°=($\sqrt{2}$-1)L,
当θ2=135°时,粒子打到挡板MN上的位置到x轴的距离为:
y2=r′+r′sin45°=($\sqrt{2}$+1)L;
答:(1)粒子在A点第二次进入磁场时,其速度方向与x轴正方向之间的夹角为45°或135°.
(2)粒子在A点第二次进入磁场时,该粒子到达挡板上时的速度大小为$\sqrt{8{v}_{0}^{2}+\frac{2qEd}{m}}$,打到挡板MN上的位置到x轴的距离为:($\sqrt{2}$-1)L、($\sqrt{2}$+1)L.
点评 本通考查了粒子在电场与磁场中的运动,解题的基本思路是:分析清楚粒子运动过程,作出粒子运动轨迹,先定圆心,由条件得半径,确定运动轨迹;第二问粒子的速度大小可以由动能定理求解,也可以由类平抛运动规律求解.

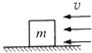 如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v0时刚好能推动该物块.已知风对物块的推力F∝Sv2,其中v为风速、S为物块迎风面积.当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )
如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v0时刚好能推动该物块.已知风对物块的推力F∝Sv2,其中v为风速、S为物块迎风面积.当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )| A. | 4m | B. | 8m | C. | 32m | D. | 64m |
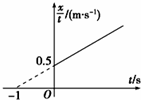 一个物体沿直线运动,从t=0时刻开始,物体的$\frac{x}{t}$-t的图象如图所示,图线与横、纵坐标轴的交点分别为-1s和0.5m/s,由此可知( )
一个物体沿直线运动,从t=0时刻开始,物体的$\frac{x}{t}$-t的图象如图所示,图线与横、纵坐标轴的交点分别为-1s和0.5m/s,由此可知( )| A. | 物体做速度大小为0.5 m/s的匀速直线运动 | |
| B. | 物体做变加速直线运动 | |
| C. | 物体做匀加速运动,加速度的大小为0.5 m/s2 | |
| D. | 物体做匀加速运动,初速度大小为0.5 m/s |
 ${\;}_{92}^{238}$U放射性衰变有多种可能途径,其中一种途径是先变成${\;}_{83}^{210}$Bi,而${\;}_{83}^{210}$Bi可以经一次衰变变成${\;}_{a}^{210}$X(X代表某种元素),也可以经一次衰变变成${\;}_{81}^{b}$Ti,${\;}_{a}^{210}$X和${\;}_{81}^{b}$Ti最后都变成${\;}_{82}^{206}$Pb,衰变路径如图所示.可知图中( )
${\;}_{92}^{238}$U放射性衰变有多种可能途径,其中一种途径是先变成${\;}_{83}^{210}$Bi,而${\;}_{83}^{210}$Bi可以经一次衰变变成${\;}_{a}^{210}$X(X代表某种元素),也可以经一次衰变变成${\;}_{81}^{b}$Ti,${\;}_{a}^{210}$X和${\;}_{81}^{b}$Ti最后都变成${\;}_{82}^{206}$Pb,衰变路径如图所示.可知图中( )| A. | a=82,b=206 | |
| B. | a=84,b=206 | |
| C. | ①是β衰变,放出电子,电子是由中子转变成质子和电子而生成的 | |
| D. | ②是α衰变,放出的是正电子,正电子是由质子转变成中子和一个正电子而生成的 | |
| E. | ${\;}_{92}^{238}$U经过8次α衰变和6次β衰变后可生成新核${\;}_{82}^{206}$Pb |
| A. | (μ1+μ2)(m1+m2)g | B. | μ1(m1+m2)g+μ2m2g | C. | (μ1+μ2)m2g | D. | (μ1m1+μ2m2)g |
| A. | 普朗克为了解释黑体辐射现象,第一次提出了能量量子化理论 | |
| B. | 爱因斯坦为了解释光电效应的规律,提出了光子说 | |
| C. | 卢瑟福通过对α粒子散射实验的研究,提出了原子的核式结构模型 | |
| D. | 贝克勒尔通过对天然放射性的研究,发现原子核是由质子和中子组成的 | |
| E. | 玻尔大胆提出假设,认为实物粒子也具有波动性 |
 某同学根据所学知识设计了如图所示加速器,给质量为m,电量为+q的小球(视为质点)加速,两固定的平行金属板上下放置,板间固定一半径为R的竖直光滑绝缘圆轨道,在轨道最高点和最低点处各有一个感应器(视为质点).某时刻小球以初速度v0从轨道最低点水平向右冲入圆轨道,感应器立刻通过控制电路在两金属板间加上大小恒定的电压,使板间产生方向竖直向上的电场强度E,且qE=2mg,之后小球每经过一次感应器感应器就通过控制电路使电场反向一次:
某同学根据所学知识设计了如图所示加速器,给质量为m,电量为+q的小球(视为质点)加速,两固定的平行金属板上下放置,板间固定一半径为R的竖直光滑绝缘圆轨道,在轨道最高点和最低点处各有一个感应器(视为质点).某时刻小球以初速度v0从轨道最低点水平向右冲入圆轨道,感应器立刻通过控制电路在两金属板间加上大小恒定的电压,使板间产生方向竖直向上的电场强度E,且qE=2mg,之后小球每经过一次感应器感应器就通过控制电路使电场反向一次: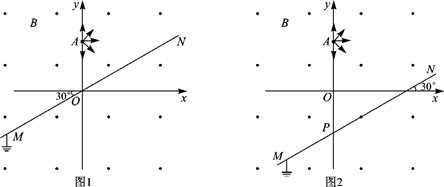
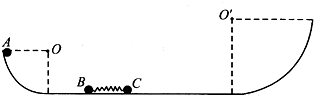 如图所示,光滑固定轨道的左端是半径为R的四分之一圆弧,右端是半径为2R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,且B、C间用一长度不变并锁定的轻弹簧拴接,弹性势能Ep=$\frac{2}{3}$mgR.一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰撞后立即粘在一起结合成D不再分离(碰撞时间极短).当D、C 一起刚要滑到右侧最低点时,弹簧锁定解除,且立即将C弹出并与弹簧分离,求:
如图所示,光滑固定轨道的左端是半径为R的四分之一圆弧,右端是半径为2R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,且B、C间用一长度不变并锁定的轻弹簧拴接,弹性势能Ep=$\frac{2}{3}$mgR.一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰撞后立即粘在一起结合成D不再分离(碰撞时间极短).当D、C 一起刚要滑到右侧最低点时,弹簧锁定解除,且立即将C弹出并与弹簧分离,求: