题目内容
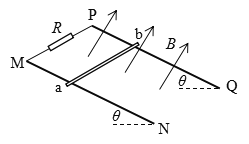
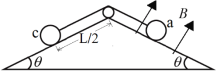
【题目】如图,两固定的光滑绝缘斜面倾角均为![]() ,上沿相连。两细金属棒ab(仅标出a端)和cd(仅标出c端)长度均为
,上沿相连。两细金属棒ab(仅标出a端)和cd(仅标出c端)长度均为![]() ,质量分别为
,质量分别为![]() 和
和![]() ;用两根不可伸长的柔软轻导线将它们连成闭合回路abdca,并通过固定在斜面上沿的两光滑绝缘小定滑轮跨放在斜面上,使两金属棒水平,金属棒cd到斜面上沿的距离为
;用两根不可伸长的柔软轻导线将它们连成闭合回路abdca,并通过固定在斜面上沿的两光滑绝缘小定滑轮跨放在斜面上,使两金属棒水平,金属棒cd到斜面上沿的距离为![]() /2。右斜面上存在匀强磁场,磁感应强度大小为
/2。右斜面上存在匀强磁场,磁感应强度大小为![]() ,方向垂直于斜面向上。已知两根软导线刚好不在磁场中,回路电阻为
,方向垂直于斜面向上。已知两根软导线刚好不在磁场中,回路电阻为![]() ,重力加速度大小为
,重力加速度大小为![]() 。已知金属棒
。已知金属棒![]() 匀速下滑,在cd运动到斜面上沿的过程中,求:
匀速下滑,在cd运动到斜面上沿的过程中,求:
(1)作用在金属棒![]() 上的安培力的大小;
上的安培力的大小;
(2)通过导体棒的电流I和通过的电荷量q
【答案】(1)![]() (2)
(2)![]() ,
,![]()
【解析】
(1)由![]() 、
、![]() 棒被平行于斜面的导线相连,故
棒被平行于斜面的导线相连,故![]() 、
、![]() 速率始终相同,既
速率始终相同,既![]() 也做匀速直线运动,
也做匀速直线运动,![]() 、
、![]() 均受平衡力作用。
均受平衡力作用。
选![]() 为研究对象,受力分析如图:
为研究对象,受力分析如图:

沿斜面方向:
![]()
选![]() 为研究对象,受力分析如图
为研究对象,受力分析如图

其沿斜面方向受力平衡:
![]()
![]() 与
与![]() 为作用力与反作用力:
为作用力与反作用力:
![]() ,
,
联立可得:
![]()
![]()
(2)
![]() ②
②
联立![]() ②式得通过导体棒的电流:
②式得通过导体棒的电流:
![]() ③
③
设感应电动势为![]() ,金属棒运动速度的大小为v,ab棒切割磁感线产生的电动势为:
,金属棒运动速度的大小为v,ab棒切割磁感线产生的电动势为:
![]()
由闭合电路欧姆定律:
![]()
联立③ ④得
![]()
cd棒到达顶部的时间为:
![]()
通过导体棒的电荷量:
![]()

练习册系列答案
相关题目