题目内容
14. 如图所示,匀速转动的水平转台上,沿半径方向放置两个用细线相连的小物块A、B(可视为质点),质量分别为mA=3kg、mB=1kg;细线长L=2m,A、B与转台间的动摩擦因数μ=0.2.开始转动时A放在转轴处,细线刚好拉直但无张力,重力加速度G=10m/s2.最大静摩擦力等于滑动摩擦力.求:
如图所示,匀速转动的水平转台上,沿半径方向放置两个用细线相连的小物块A、B(可视为质点),质量分别为mA=3kg、mB=1kg;细线长L=2m,A、B与转台间的动摩擦因数μ=0.2.开始转动时A放在转轴处,细线刚好拉直但无张力,重力加速度G=10m/s2.最大静摩擦力等于滑动摩擦力.求:(1)使细线刚好拉直但无张力,转台转动的最大角速度ω1为多少;
(2)使A、B能随转台一起匀速圆周运动,转台转动的最大角速度ω2为多少.
分析 细绳的弹力刚好为零,B与转台间摩擦力恰好达最大静摩擦力,且提供向心力$μ{m}_{B}g={m}_{B}L{{ω}_{1}}^{2}$,代入数据可以计算出此时的最大角速度.
A、B与转台间摩擦力都达最大静摩擦力,分别对A和B受力分析,根据牛顿第二定律列方程计算此时的角速度.
解答 解:(1)当转台角速度为ω1时,B与转台间摩擦力恰好达最大静摩擦力,细绳的弹力刚好为零;有:$μ{m}_{B}g={m}_{B}L{{ω}_{1}}^{2}$
带入数值解得:ω1=1rad/s
(2)当转台角速度为ω2时,A、B与转台间摩擦力都达最大静摩擦力,则:
对A有:μmAg=T; 对B有:$T+μ{m}_{B}g={m}_{B}L{{ω}_{2}}^{2}$
带入数值解得:ω2=2rad/s
答:(1)使细线刚好拉直但无张力,转台转动的最大角速度ω1为1rad/s;
(2)使A、B能随转台一起匀速圆周运动,转台转动的最大角速度ω2为2rad/s.
点评 本题考查圆周运动中力与运动的关系,注意本题中为静摩擦力与绳子的拉力充当向心力,故应注意静摩擦力是否已达到最大静摩擦力.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
15.示波管是一种多功能电学仪器,其有一发光点S位于平面镜前,请作图确定人眼在什么范围内可看到S的像.结构如图所示,电子枪中的炽热金属丝不断放出可认为初速度为零的电子,在加速电场加速,再经偏转电极XX′和YY′,最后在荧光屏上形成图象,现在偏转电极XX′和YY′上不加电压,加速电场电压∪,经加速后形成横截面积为S,电流为j的电子束,已知电子的电荷量为e,质量为m,则在刚射出加速电场时,一小段长为△L的电子束内电子个数是( )


| A. | $\frac{I△L}{e}$$\sqrt{\frac{m}{2eU}}$ | B. | $\frac{I△L}{eS}$$\sqrt{\frac{m}{2eU}}$ | C. | $\frac{1}{eS}$$\sqrt{\frac{m}{2eU}}$ | D. | $\frac{IS△L}{e}$$\sqrt{\frac{m}{2eU}}$ |
5.物体在倾角为θ的斜面上静止,当θ减小时,物体受到的支持力N和摩擦力f的变化情况是( )
| A. | N减小,f增大 | B. | N增大,f减小 | C. | N增大,f不变 | D. | N不变,f增大 |
2. 一质量为m的物体静止在水平地面上,在水平拉力F的作用下开始运动,在0~6s内其速度与时间关系图象和拉力的功率与时间关系图象如图所示,取g=10m/s2,下列判断正确的是( )
一质量为m的物体静止在水平地面上,在水平拉力F的作用下开始运动,在0~6s内其速度与时间关系图象和拉力的功率与时间关系图象如图所示,取g=10m/s2,下列判断正确的是( )
 一质量为m的物体静止在水平地面上,在水平拉力F的作用下开始运动,在0~6s内其速度与时间关系图象和拉力的功率与时间关系图象如图所示,取g=10m/s2,下列判断正确的是( )
一质量为m的物体静止在水平地面上,在水平拉力F的作用下开始运动,在0~6s内其速度与时间关系图象和拉力的功率与时间关系图象如图所示,取g=10m/s2,下列判断正确的是( )| A. | 拉力F的大小为10N,且保持不变 | B. | 物体的质量m为3kg | ||
| C. | 0~6s内物体克服摩擦力做功24J | D. | 0~6s内拉力做的功为156J |
9. 倾角为θ、质量为M的斜面体静止在粗糙水平面上,质量为m的滑块静止在斜面体上,滑块与斜面体间动摩擦因数为μ,重力加速度为g;如图所示.下列结论正确的是( )
倾角为θ、质量为M的斜面体静止在粗糙水平面上,质量为m的滑块静止在斜面体上,滑块与斜面体间动摩擦因数为μ,重力加速度为g;如图所示.下列结论正确的是( )
 倾角为θ、质量为M的斜面体静止在粗糙水平面上,质量为m的滑块静止在斜面体上,滑块与斜面体间动摩擦因数为μ,重力加速度为g;如图所示.下列结论正确的是( )
倾角为θ、质量为M的斜面体静止在粗糙水平面上,质量为m的滑块静止在斜面体上,滑块与斜面体间动摩擦因数为μ,重力加速度为g;如图所示.下列结论正确的是( )| A. | 滑块受到的摩擦力大小一定是μmgcosθ | |
| B. | 滑块对斜面体的作用力为mg | |
| C. | 地面对斜面体有水平向右的摩擦力 | |
| D. | 若只是增大滑块的质量,其它条件不变,释放滑块后,滑块可能沿斜面下滑 |
6.在研究两个共点力的合力实验中,得出F合随夹角θ变化的规律如图,则两个分力大小分别为( )


| A. | 16N、12N | B. | 16N、7N | C. | 8N、6N | D. | 28N、7N |
4.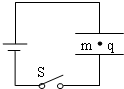 如图所示,两板间距为d的平行板电容器与一电源连接,开关S闭合,电容器两板间有一质量为m,带电荷量为q的微粒静止不动,下列叙述中正确的是( )
如图所示,两板间距为d的平行板电容器与一电源连接,开关S闭合,电容器两板间有一质量为m,带电荷量为q的微粒静止不动,下列叙述中正确的是( )
 如图所示,两板间距为d的平行板电容器与一电源连接,开关S闭合,电容器两板间有一质量为m,带电荷量为q的微粒静止不动,下列叙述中正确的是( )
如图所示,两板间距为d的平行板电容器与一电源连接,开关S闭合,电容器两板间有一质量为m,带电荷量为q的微粒静止不动,下列叙述中正确的是( )| A. | 微粒带的是正电 | |
| B. | 电源电动势的大小大于$\frac{mgd}{q}$ | |
| C. | 断开开关S,把电容器两极板间距离增大微粒将向下做加速运动 | |
| D. | 保持开关S闭合,把电容器两极板间距离增大微粒将向下做加速运动 |




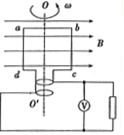 交流发电机转子有n匝线圈,每匝线圈所围面积为S,匀强磁场的磁感应强度为B,匀速转动的角速度为ω,线圈电阻为r,外电路电阻为R,当线圈处于中性面时开始计时,逆时针匀速转动180°过程中,求:
交流发电机转子有n匝线圈,每匝线圈所围面积为S,匀强磁场的磁感应强度为B,匀速转动的角速度为ω,线圈电阻为r,外电路电阻为R,当线圈处于中性面时开始计时,逆时针匀速转动180°过程中,求: