题目内容
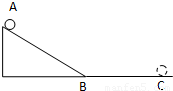
如图所示，一质量为2kg的小球从斜面顶点A由静止开始向下运动，经过斜面底端B点后在水平面上运动，最后停止在C点．已知斜面长为18m，斜面的倾角为37°，小球与斜面、水平面的动摩擦因数均为0.25，g=10m/s2，sin37°=0.6，不计小球从斜面进入水平面时机械能的损失．求：（1）小球通过B点时的速度大小．
（2）小球在水平面上运动的位移大小．
【答案】分析：先分析物体的受力情况，根据牛顿第二定律求出物体在斜面上和水平面上的加速度大小，再应用运动学速度、位移关系公式求出通过B点时的速度大小和小球在水平面上运动的位移大小．
解答：解：（1）由牛顿第二定律得：mgsin37°-µmg cos37°=ma1
a1=g（sin37°-µ cos37°）=4m/s2
由 v2-0=2ax1，得
v=
=12m/s
（2）设小球在水平面上运动的加速度大小为为a2，
则µmg=ma2
a2=μg=2.5 m/s2
又由 0-v2=-2ax2 代入数据解得：x2=28.8m
答：（1）小球通过B点时的速度大小为12m/s．
（2）小球在水平面上运动的位移大小28.8m．
点评：本题也可运用动能定理求出，过程比牛顿定律和运动学公式结合应用更为简洁方便．两种方法对比发现，当涉及力在空间的累积效应时，可优先考虑动能定理．
解答：解：（1）由牛顿第二定律得：mgsin37°-µmg cos37°=ma1
a1=g（sin37°-µ cos37°）=4m/s2
由 v2-0=2ax1，得
v=
=12m/s （2）设小球在水平面上运动的加速度大小为为a2，
则µmg=ma2
a2=μg=2.5 m/s2
又由 0-v2=-2ax2 代入数据解得：x2=28.8m
答：（1）小球通过B点时的速度大小为12m/s．
（2）小球在水平面上运动的位移大小28.8m．
点评：本题也可运用动能定理求出，过程比牛顿定律和运动学公式结合应用更为简洁方便．两种方法对比发现，当涉及力在空间的累积效应时，可优先考虑动能定理．
练习册系列答案
金钥匙试卷系列答案
相关题目
如图所示，一质量为m、带电量为q的小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线向左与竖直方向成θ角，重力加速度为g．
（2012?增城市模拟）如图所示，一质量为m=2kg的小球以某一初速度v0=8m/s向壕沟运动，小球开始运动时距离壕沟上边缘L=8m，地面粗糙有摩擦．小球恰好飞过壕沟，已知壕沟长s=1.6m，落差h=0.8m．求：
