Question

（10分）物体在斜面顶端由静止开始下滑作匀加速直线运动，已知在头4秒内位移为L，在最后4秒内位移为4L，则总的运动时间是多少？在整个过程中的位移是多少？

 

Answer 1

【答案】

(25/4) S     或者 6.25S

【解析】加速度为a，总时间为T

头4秒内位移是S

即： S = 0.5 • a • 4²

 

最后4秒内位移为4S

最后4秒内位移 = 前T秒的位移（全程）- 前（T-4）秒的位移

即：

4S = 0.5 • a • T² - 0.5 • a • (T-4)²

把  S = 0.5 • a • 4² 带入上式得：

4 • 0.5 • a • 4² = 05 • a • T² - 0.5 • a • (T-4)²

将式中的【0.5 • a】约去 得：

4 • 4² = T² - (T-4)²

64 =  T² - (T² - 8T + 16)

64 = 8T - 16

T = 10 秒

由 S = 0.5 • a • 4² 

S = 8 a 

得 加速度 a = S/8

整个过程中的位移 X = 0.5 • a • T² 

= 0.5 • S/8 • 10² 

= (25/4) S     或者 6.25S

本题考查匀加速直线运动推论的应用，由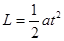可求得加速度大小，根据平均速度等于中间时刻的瞬时速度，可求得第一个L中间时刻的瞬时速度，最后4s内的中间时刻的瞬时速度，再由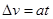可求得时间间隔t，从而求得总的运动时间，再由位移与时间的关系式可求得总位移