题目内容
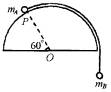
如图所示，细而轻的绳两端，分别系有质量为mA、mB的球，mA静止在光滑半球形表面P点，已知过P点的半径与水平面夹角为60°，则mA和mB的关系是( )
A．mA=mB
B．mA=
mB
C．mA=2mB
D．mB=
mA
答案：C
解析：
提示：
解析：
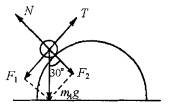
分析mB受力可知T=mBg 分析mA受力如图所示，有重力mAg、支持力N、绳拉力T，把重力沿另外两个力的反方向正交分解 F1=mAgsin30° T=F1=mAgsin30°=mBg 得mA=2mB
|
提示：
连接两质点的细而轻的绳，不计其重力，而沿半球表面，细绳对mA的拉力认为是沿OP半径垂线方向，也就是半径的切线方向．
|
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图所示，细而轻的绳两端，分别系有质量为mA、mB的球，mA静止在光滑半球形表面P点（球可视为质点），已知过P点的半径与水平面夹角为60°，则mA和mB的关系是（ ）
如图所示，细而轻的绳两端，分别系有质量为m1、m2的球，m1静止在光滑半球形表面P点，已知过P点的半径与水平面夹角为45°，则m1和m2的关系是（ ）
B．
D．
B．
D．