题目内容
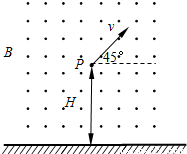 如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场.匀强磁场的磁感应强度为B,方向水平并垂直纸面向外,一质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀速圆周运动.(重力加速度为g)
如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场.匀强磁场的磁感应强度为B,方向水平并垂直纸面向外,一质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀速圆周运动.(重力加速度为g)(1)求此区域内电场强度的大小和方向;
(2)若某时刻微粒运动到场中距地面高度为H的P点,速度与水平方向成45,如图所示.则该微粒至少须经多长时间运动到距地面最高点?最高点距地面多高?
(3)在(2)问中微粒运动P点时,突然撤去磁场,同时电场强度大小不变,方向变为水平向右,则该微粒运动中距地面的最大高度是多少?
【答案】分析:(1)带电粒子在电场和磁场及重力场能做匀速圆周运动,则有电场力与重力平衡,而洛伦兹力提供向心力.从而根据平衡条件可确定电场强度的大小与方向;
(2)由粒子所受洛伦兹力提供向心力,从而求出运动圆弧的半径与周期,再根据几何关系来确定圆弧最高点与地面的高度及运动时间;
(3)当撤去磁场时,粒子受到重力与电场力作用,从而做曲线运动.因此此运动可看成竖直方向与水平方向两个分运动,运用动能定理可求出竖直的高度,最终可算出结果.
解答: 解:(1)带电微粒在做匀速圆周运动,电场力与重力应平衡,有mg=Eq,即E=
解:(1)带电微粒在做匀速圆周运动,电场力与重力应平衡,有mg=Eq,即E=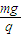 ,方向竖直向下.
,方向竖直向下.
(2)粒子做匀速圆周运动,轨道半径为R,如图所示.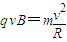 ,
,
根据几何关系可确定,最高点与地面的距离为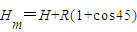 ,
,
解得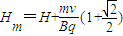 .
.
该微粒运动周期为T=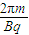 ,
,
根据运动圆弧对应的圆心角,可得粒子运动至最高点所用时间为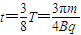 .
.
(3)设粒子上升高度为h,由动能定理得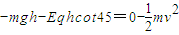 ,
,
解得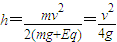 .
.
微粒离地面最大高度为H+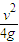 .
.
答:(1)求此区域内电场强度的大小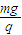 和方向为竖直向下;
和方向为竖直向下;
(2)该微粒至少须经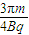 时间运动到距地面最高点;最高点距地面高度为
时间运动到距地面最高点;最高点距地面高度为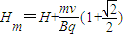
(3)该微粒运动中距地面的最大高度是H+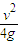 .
.
点评:运用共点力平衡条件、牛顿第二定律、动能定理等规律,及由洛伦兹力提供向心力来确定线速度大小与周期.同时借助于数学的几何关系来确定已知长度与圆弧半径的关系.
(2)由粒子所受洛伦兹力提供向心力,从而求出运动圆弧的半径与周期,再根据几何关系来确定圆弧最高点与地面的高度及运动时间;
(3)当撤去磁场时,粒子受到重力与电场力作用,从而做曲线运动.因此此运动可看成竖直方向与水平方向两个分运动,运用动能定理可求出竖直的高度,最终可算出结果.
解答:
 解:(1)带电微粒在做匀速圆周运动,电场力与重力应平衡,有mg=Eq,即E=
解:(1)带电微粒在做匀速圆周运动,电场力与重力应平衡,有mg=Eq,即E=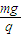 ,方向竖直向下.
,方向竖直向下.(2)粒子做匀速圆周运动,轨道半径为R,如图所示.
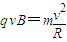 ,
,根据几何关系可确定,最高点与地面的距离为
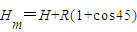 ,
,解得
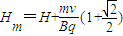 .
.该微粒运动周期为T=
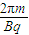 ,
,根据运动圆弧对应的圆心角,可得粒子运动至最高点所用时间为
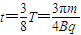 .
.(3)设粒子上升高度为h,由动能定理得
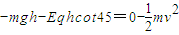 ,
,解得
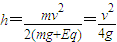 .
.微粒离地面最大高度为H+
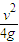 .
.答:(1)求此区域内电场强度的大小
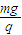 和方向为竖直向下;
和方向为竖直向下;(2)该微粒至少须经
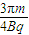 时间运动到距地面最高点;最高点距地面高度为
时间运动到距地面最高点;最高点距地面高度为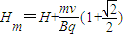
(3)该微粒运动中距地面的最大高度是H+
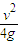 .
.点评:运用共点力平衡条件、牛顿第二定律、动能定理等规律,及由洛伦兹力提供向心力来确定线速度大小与周期.同时借助于数学的几何关系来确定已知长度与圆弧半径的关系.

练习册系列答案
相关题目
 如图所示,在地面附近的电场中,一条沿竖直方向的电场线上有A、B两点.若将带电液滴从A点由静止释放,带电液滴将沿竖直方向下落,到达B点时的速度恰好为零(不考虑空气阻力),则( )
如图所示,在地面附近的电场中,一条沿竖直方向的电场线上有A、B两点.若将带电液滴从A点由静止释放,带电液滴将沿竖直方向下落,到达B点时的速度恰好为零(不考虑空气阻力),则( )| A、液滴一定做匀变速运动 | B、A点的电势一定比B点高 | C、电场中A点场强一定大于B点的场强 | D、液滴由A运动到B的过程中,重力势能的减少量等于电势能的增加量 |
 如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场(图中均未画出).磁感应强度为B,方向水平并垂直纸面向外.一质量为m、带电量为-q的带电微粒在此区域竖直平面内恰好作速度大小为v的匀速圆周运动.(重力加速度为g)
如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场(图中均未画出).磁感应强度为B,方向水平并垂直纸面向外.一质量为m、带电量为-q的带电微粒在此区域竖直平面内恰好作速度大小为v的匀速圆周运动.(重力加速度为g) (2011?武汉模拟)如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场.匀强磁场的磁感应强度为B,方向水平并垂直纸面向外,一质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀速圆周运动.(重力加速度为g)
(2011?武汉模拟)如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场.匀强磁场的磁感应强度为B,方向水平并垂直纸面向外,一质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀速圆周运动.(重力加速度为g) 如图所示,在地面附近,坐标系Oxy在竖直平面内,空间有沿水平方向垂直于纸面向里的匀强磁场,磁感应强度大小为B,在x<0的空间内还有沿x轴负方向的匀强电场,一个质量为m的带电量为q的油滴途经图中M(-a,0)点(a>0),沿着与水平方向成α角斜向下做匀速直线运动,进入x>0的区域,求:
如图所示,在地面附近,坐标系Oxy在竖直平面内,空间有沿水平方向垂直于纸面向里的匀强磁场,磁感应强度大小为B,在x<0的空间内还有沿x轴负方向的匀强电场,一个质量为m的带电量为q的油滴途经图中M(-a,0)点(a>0),沿着与水平方向成α角斜向下做匀速直线运动,进入x>0的区域,求: