题目内容
长为L、粗细均匀的细杆AB质量为m，在距A端L/3的O处用一钉子钉在竖直墙上，细杆可绕钉子在竖直平面内无摩擦转动，今在细杆上端A施加一水平力F，使细杆偏离竖直方向成θ 角，（θ＜45°）且平衡，如图所示，则水平力F的力矩大小是 ，增大F使偏角变为2θ，此时细杆仍处于平衡状态，则此时力F的大小是 ．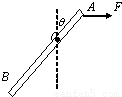
【答案】分析：力矩等于力与力臂的乘积，力臂是支点到力的作用线的距离，根据杠杆平衡条件，即可求解．
解答：解：偏角为θ时，F的力臂是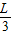
COSθ，故F的力矩是F×
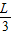COSθ．
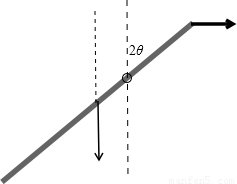由杠杆平衡条件得：
mg×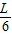
sinθ=F×
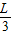cosθ
偏角变为2θ时，如图根据杠杆平衡条件，
mg×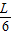
sin2θ=F×
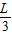cos2θ，
故F=
mgtan2θ
故答案是：
mgLsinθ；
mgtan2θ
点评：此题为杠杆模型，关键是找到力臂，运用杠杆的平衡条件来解题．
解答：解：偏角为θ时，F的力臂是
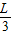COSθ，故F的力矩是F×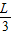COSθ．由杠杆平衡条件得：mg×
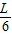sinθ=F×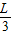cosθ偏角变为2θ时，如图根据杠杆平衡条件，
mg×
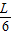sin2θ=F×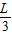cos2θ，故F=
mgtan2θ故答案是：
mgLsinθ；mgtan2θ点评：此题为杠杆模型，关键是找到力臂，运用杠杆的平衡条件来解题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
长为L、粗细均匀的细杆AB质量为m，在距A端L/3的O处用一钉子钉在竖直墙上，细杆可绕钉子在竖直平面内无摩擦转动，今在细杆上端A施加一水平力F，使细杆偏离竖直方向成θ 角，（θ＜45°）且平衡，如图所示，则水平力F的力矩大小是
一根长为L、粗细均匀的轻绳，两端分别固定在天花板上的A、B两点．若在细绳的C处悬一重物，如图所示，则下列说法中正确的是（ ）
