题目内容
5. 在x轴上有两个点电荷q1和q2(q1在q2的左边),x轴上每一点的电势随着x变化的关系如图所示.当x=x0时,电势为0;当x=x1时,电势有最小值(点电荷产生的电势公式为φ=k$\frac{q}{r}$).
在x轴上有两个点电荷q1和q2(q1在q2的左边),x轴上每一点的电势随着x变化的关系如图所示.当x=x0时,电势为0;当x=x1时,电势有最小值(点电荷产生的电势公式为φ=k$\frac{q}{r}$).(1)分析两个电荷的带电性质;
(1)求两个电荷的位置坐标;
(2)求两个电荷的电量之比.
分析 根据顺着电场线方向电势降低,确定出两电荷的电性.由图知当x=x0时,电势为零,由电场的叠加原理求出两电荷的位置,并求解两个电荷的比值.
解答 解:由图知:x从0到∞,电势先降低后升高,则知q2是正电荷,在x轴上坐标原点;q1是负电荷,在x轴的负方向上.
设坐标为x,由图得:k$\frac{{q}_{2}}{{x}_{0}}$+$\frac{k{q}_{1}}{{x}_{0}-x}$=0;
$\frac{k{q}_{2}}{{x}_{1}^{2}}$+$\frac{k{q}_{1}}{({x}_{1}-x)^{2}}$=0
联立方程解得:x=$2{x}_{1}-\frac{{x}_{1}^{2}}{{x}_{0}}$,$\frac{{q}_{1}}{{q}_{2}}$=$-\frac{({x}_{1}-{x}_{0})^{2}}{{x}_{0}^{2}}$
答:(1)分析两个电荷的带电性质,q2电荷,在x轴上坐标原点;q1是负电荷,;
(1)求两个电荷的位置坐标q2电在x轴上坐标原点;q1在$2{x}_{1}-\frac{{x}_{1}^{2}}{{x}_{0}}$;
(2)求两个电荷的电量之比$-\frac{({x}_{1}-{x}_{0})^{2}}{{x}_{0}^{2}}$
点评 本题信息给予题,关键要抓住题干中有效信息和图象中有效信息,利用叠加原理分析,灵活应用电势的公式和斜率为零.

练习册系列答案
相关题目
16.地球同步卫星离地心距离为r,运行速率为v1,加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则( )
| A. | $\frac{a_1}{a_2}$=$\frac{r}{R}$ | B. | $\frac{a_1}{a_2}$=$\frac{R^2}{r^2}$ | C. | $\frac{v_1}{v_2}$=$\frac{R^2}{r^2}$ | D. | $\frac{v_1}{v_2}$=$\sqrt{\frac{r}{R}}$ |
17. 如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )
如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )
 如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )
如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )| A. | 向右做匀加速直线运动 | B. | 向左做匀加速直线运动 | ||
| C. | 向右做匀速直线运动 | D. | 向左做匀减速直线运动 |
14.一辆汽车运动的v-t图象如图,则汽车在0~2s内和2s~3s内相比( )
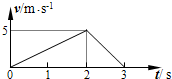

| A. | 位移大小相等 | B. | 平均速度相等 | C. | 速度变化相同 | D. | 运动方向相同 |
15. 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )| A. | 圆形线圈中的磁场可以是向上均匀减弱 | |
| B. | 导体棒ab受到的安培力大小为mgsinθ | |
| C. | 回路中的感应电流为$\frac{mgtanθ}{{B}_{2}d}$ | |
| D. | 圆形导线中的电热功率为$\frac{{m}^{2}{g}^{2}rta{n}^{2}θ}{{{B}_{2}}^{2}{d}^{2}}$ |
 如图所示,两个半径为R的四分之一圆弧构成的光滑细管道ABC竖直放置,且固定在光滑水平面上,圆心连线O1O2水平.轻弹簧左端固定在竖直挡板上,右端与质量为m的小球接触(不拴接,小球的直径略小于管道内径),开始时弹簧处于锁定状态,具有一定的弹性势能,重力加速度为g.解除锁定,小球离开弹簧后进入管道.
如图所示,两个半径为R的四分之一圆弧构成的光滑细管道ABC竖直放置,且固定在光滑水平面上,圆心连线O1O2水平.轻弹簧左端固定在竖直挡板上,右端与质量为m的小球接触(不拴接,小球的直径略小于管道内径),开始时弹簧处于锁定状态,具有一定的弹性势能,重力加速度为g.解除锁定,小球离开弹簧后进入管道. 如图所示,一根有一定电阻的直导体棒质量为m、长为L,其两端放在位于水平面内间距也为L的光滑平行导轨上,并与之接触良好;棒左侧两导轨之间连接一可控电阻;导轨置于匀强磁场中,磁场的磁感应强度大小为B,方向垂直于导轨所在平面.t=0时刻,给导体棒一个平行于导轨的初速度,此时可控电阻的阻值为R0.在棒运动过程中,通过可控电阻的变化使棒中的电流强度保持恒定.不计导轨电阻,导体棒一直在磁场中
如图所示,一根有一定电阻的直导体棒质量为m、长为L,其两端放在位于水平面内间距也为L的光滑平行导轨上,并与之接触良好;棒左侧两导轨之间连接一可控电阻;导轨置于匀强磁场中,磁场的磁感应强度大小为B,方向垂直于导轨所在平面.t=0时刻,给导体棒一个平行于导轨的初速度,此时可控电阻的阻值为R0.在棒运动过程中,通过可控电阻的变化使棒中的电流强度保持恒定.不计导轨电阻,导体棒一直在磁场中