题目内容
20.嫦娥一号是我国研制的首颗绕月人造卫星,设嫦娥一号贴着月球表面做匀速圆周运动,经过时间t (t小于嫦娥一号的绕行周期),嫦娥一号运动的弧长为s,嫦娥一号与月球中心的连线扫过角度为θ(θ为弧度制表示),引力常量为G,则下面描述错误的是( )| A. | 航天器的轨道半径为$\frac{s}{θ}$ | B. | 航天器的环绕周期为$\frac{2πt}{θ}$ | ||
| C. | 月球的质量为$\frac{{s}^{2}}{Gθ{t}^{2}}$ | D. | 月球的密度为$\frac{3{θ}^{2}}{4G{t}^{2}}$ |
分析 根据弧长与半径、角度的关系求出航天器的轨道半径.根据转过的角度求出角速度,从而得出航天器的周期.根据万有引力提供向心力,结合线速度的大小求出月球的质量,根据密度公式求出月球的密度.
解答 解:A、在t时间内穿过的弧长为s,转过的角度为θ,根据s=rθ知,航天器的轨道半径r=$\frac{s}{θ}$,故A正确.
B、航天器的角速度$ω=\frac{θ}{t}$,则周期T=$\frac{2π}{ω}=\frac{2πt}{θ}$,故B正确.
C、航天器的线速度v=$\frac{s}{t}$,根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$得,月球的质量M=$\frac{{v}^{2}r}{G}=\frac{{s}^{3}}{{Gt}^{2}θ}$,故C错误.
D、航天器贴着月球表面运行,轨道半径等于月球的半径,月球的密度$ρ=\frac{M}{V}$=$\frac{\frac{{s}^{3}}{G{t}^{2}θ}}{\frac{4}{3}π{r}^{3}}$=$\frac{3{θ}^{2}}{4πG{t}^{2}}$,故D错误.
本题选择不正确的,故选:CD.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道线速度、角速度、周期、轨道半径之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.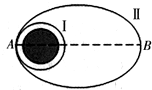 2015年3月,美国宇航局的“信使”号水星探测器按计划将陨落在水星表面,工程师找到了一种聪明的办法,能够使其寿命再延长一个月.这个办法就是通过向后释放推进系统中的高压氮气来提升轨道.如图所示,设释放氮气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氮气后探测器进入椭圆轨道Ⅱ上,忽略探测器在椭圆轨道上所受外界阻力.则下列说法正确的是( )
2015年3月,美国宇航局的“信使”号水星探测器按计划将陨落在水星表面,工程师找到了一种聪明的办法,能够使其寿命再延长一个月.这个办法就是通过向后释放推进系统中的高压氮气来提升轨道.如图所示,设释放氮气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氮气后探测器进入椭圆轨道Ⅱ上,忽略探测器在椭圆轨道上所受外界阻力.则下列说法正确的是( )
 2015年3月,美国宇航局的“信使”号水星探测器按计划将陨落在水星表面,工程师找到了一种聪明的办法,能够使其寿命再延长一个月.这个办法就是通过向后释放推进系统中的高压氮气来提升轨道.如图所示,设释放氮气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氮气后探测器进入椭圆轨道Ⅱ上,忽略探测器在椭圆轨道上所受外界阻力.则下列说法正确的是( )
2015年3月,美国宇航局的“信使”号水星探测器按计划将陨落在水星表面,工程师找到了一种聪明的办法,能够使其寿命再延长一个月.这个办法就是通过向后释放推进系统中的高压氮气来提升轨道.如图所示,设释放氮气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氮气后探测器进入椭圆轨道Ⅱ上,忽略探测器在椭圆轨道上所受外界阻力.则下列说法正确的是( )| A. | 探测器在轨道Ⅰ和轨道Ⅱ上A点加速度大小不同 | |
| B. | 探测器在轨道Ⅰ上A点运行速度小于在轨道Ⅱ上B点速率 | |
| C. | 探测器在轨道Ⅱ上某点的速率可能等于在轨道Ⅰ上速率 | |
| D. | 探测器在轨道Ⅱ上远离水星过程中,引力势能和动能都减少 |
8.如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,则( )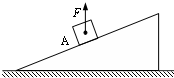

| A. | 物体A所受合力不变 | B. | 斜面对物体A的支持力不变 | ||
| C. | 斜面对物体A的摩擦力不变 | D. | 斜面对地面的支持力压力减小 |
15.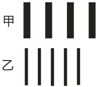 a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
 a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )| A. | a光的频率比b光大 | B. | b光比a光易发生衍射现象 | ||
| C. | a光比b光易发生全反射现象 | D. | b光在水中的传播速度较小 |
5. 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )| A. | 斜面实验是一个用来研究V与t成正比的猜想是否正确 | |
| B. | 斜面实验放大了重力的作用,便于测量小球运动的路程 | |
| C. | 通过对斜面实验的观察与计算,直接得到落体运动的规律 | |
| D. | 不直接做落体实验是因为当时时间测量不够精确 |
12.下列表述正确的是( )
| A. | ${\;}_{2}^{4}$H+${\;}_{7}^{14}$N→${\;}_{8}^{17}$O+X中,X表示${\;}_{2}^{3}$He | |
| B. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是重核裂变的核反应方程 | |
| C. | 放射性元素的半衰期与原子所处的化学状态无关 | |
| D. | β衰变中放出的β射线是核外电子挣脱原子核的束缚而形成的 |
9.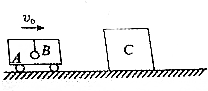 如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )
如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )
 如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )
如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )| A. | 碰撞瞬间A、C组成的系统机械能守恒 | |
| B. | 碰撞瞬间A、C组成的系统水平方向动量守恒 | |
| C. | 碰撞后的瞬间,细线拉力与小球所受重力大小相等 | |
| D. | 碰撞后的瞬间,细线拉力大于小球所受的重力 |
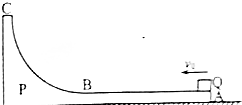 如图所示,质量为M=2kg的滑块P静止在光滑水平地面上,滑片P的AB段水平且粗糙,BC段为半径R=0.2m的光滑$\frac{1}{4}$弧面,AB部分的长度L=2m,一质量为m=1kg的小滑块Q以v0=6m/s的速度从A端滑入P,恰能滑到最高点C处,由C处返回后,最终停在AB之间的某一位置、取g=10m/s2,求;
如图所示,质量为M=2kg的滑块P静止在光滑水平地面上,滑片P的AB段水平且粗糙,BC段为半径R=0.2m的光滑$\frac{1}{4}$弧面,AB部分的长度L=2m,一质量为m=1kg的小滑块Q以v0=6m/s的速度从A端滑入P,恰能滑到最高点C处,由C处返回后,最终停在AB之间的某一位置、取g=10m/s2,求;