题目内容
5. 如图所示,某透明液体深1m,一束光线与水平面成30°角从空气斜射向该液体,进入该液体的光线与水平面的夹角为45°.(光在真空中的速率c=3.0×108m/s),则该液体的折射率n=$\frac{\sqrt{6}}{2}$,进入液体的光线射到底面所需的时间为$\frac{\sqrt{3}}{3}$×10-8s.
如图所示,某透明液体深1m,一束光线与水平面成30°角从空气斜射向该液体,进入该液体的光线与水平面的夹角为45°.(光在真空中的速率c=3.0×108m/s),则该液体的折射率n=$\frac{\sqrt{6}}{2}$,进入液体的光线射到底面所需的时间为$\frac{\sqrt{3}}{3}$×10-8s.
分析 由题图知入射角i=60°,折射角r=45°,根据折射定律求解该液体的折射率;由几何知识求出光在液体中传播的距离S,由v=$\frac{c}{n}$求出光在液体中传播的速度v,根据公式t=$\frac{S}{v}$求出传播的时间.
解答 解:根据几何知识可知,入射角 i=60°,折射角 r=45°,根据折射定律得:
n=$\frac{sini}{sinr}$=$\frac{sin60°}{sin45°}$=$\frac{\sqrt{6}}{2}$
光在液体中传播的速度为:v=$\frac{c}{n}$
光线射到底面时传播的距离为:S=$\frac{h}{cosr}$=$\sqrt{2}$h
所以进入液体的光线射到底面所需的时间:t=$\frac{S}{v}$=$\frac{\sqrt{2}nh}{c}$=$\frac{\sqrt{2}×\frac{\sqrt{6}}{2}×1}{3×1{0}^{8}}$=$\frac{\sqrt{3}}{3}$×10-8s
故答案为:$\frac{\sqrt{6}}{2}$,$\frac{\sqrt{3}}{3}$×10-8.
点评 本题是几何光学中基本问题,是折射定律和光速公式的应用,要注意入射角和折射角都是指光线与光线的夹角,不是与界面的夹角.

练习册系列答案
相关题目
3.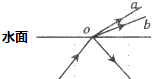 a、b两种单色光形成细光束从水中射向水面,形成两束折射光和一束反射光,如图所示.下列说法正确的是( )
a、b两种单色光形成细光束从水中射向水面,形成两束折射光和一束反射光,如图所示.下列说法正确的是( )
 a、b两种单色光形成细光束从水中射向水面,形成两束折射光和一束反射光,如图所示.下列说法正确的是( )
a、b两种单色光形成细光束从水中射向水面,形成两束折射光和一束反射光,如图所示.下列说法正确的是( )| A. | a光的折射率大 | |
| B. | a光在水中的传播速度大 | |
| C. | 保持入射点不变,顺时针方向旋转入射光,则b光先消失 | |
| D. | 保持入射点不变,逆时针方向旋转入射光,则反射光旋转的角速度大于入射光的角速度. | |
| E. | 在空气中,a、b光分别通过同一双缝干涉装置,a光的相邻亮条纹间距大 |
16.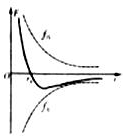 分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )
分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )
 分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )
分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )| A. | 当r=r0时,分子力为零,分子势能最大 | |
| B. | 当r<r0时,随r减小,分子力增大,分子势能减小 | |
| C. | 当r>r0时,随r增大,分子力减小,分子势能增大 | |
| D. | 当r>r0时,随r增大,分子力先增大后减小,分子势能增大 |
20. 质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )
质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )
 质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )
质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )| A. | 物体的合运动是匀加速直线运动 | B. | 物体所受的合外力为12N | ||
| C. | 物体的初速度大小为4m/s | D. | 1s末物体速度大小为5m/s |
10. 如图所示为“研究电磁感应现象”的实验装置,
如图所示为“研究电磁感应现象”的实验装置,
(1)将线圈A插入线圈B中,合上开关S,能使线圈B中感应电流的磁场方向与线圈A中原磁场方向相反的实验操作是AC;
(2)某同学第一次将滑动变阻器的触头从变阻器的左端快速滑到右端,第二次将滑动变阻器的触头从变阻器的左端慢慢滑到右端,发现电流计的指针摆动的幅度大小不同,第一次比第二次的幅度大(填写“大”或“小”),原因是线圈中的磁通量变化率(填写“磁通量”或“磁通量的变化”或“磁通量变化率”)第一次比第二次的大.
 如图所示为“研究电磁感应现象”的实验装置,
如图所示为“研究电磁感应现象”的实验装置,(1)将线圈A插入线圈B中,合上开关S,能使线圈B中感应电流的磁场方向与线圈A中原磁场方向相反的实验操作是AC;
| A.插入铁芯F | B.拔出线圈A |
| C.使变阻器阻值R变小 | D.断开开关S |
 在研究平抛运动实验中,实验室准备了下列器材:铁架台、斜槽、竖直挡板、有水平卡槽的木板、白纸、复写纸、图钉、小球、刻度尺等.部分的实验步骤如下:
在研究平抛运动实验中,实验室准备了下列器材:铁架台、斜槽、竖直挡板、有水平卡槽的木板、白纸、复写纸、图钉、小球、刻度尺等.部分的实验步骤如下: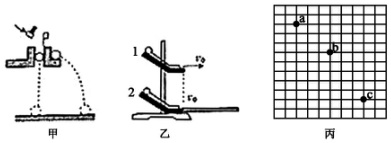
 如图所示,长为4m的水平轨道AB,与半径为R=0.5m的竖直的半圆弧轨道BC在B处相连接,有-质量为2kg的滑块(可视为质点),在水平向右、大小为14N的恒力F作用下,从A点由静止开始运动到B点,滑块与AB间的动摩擦因数为μ=0.25,BC 间粗糙,取g=10m/s2.求:
如图所示,长为4m的水平轨道AB,与半径为R=0.5m的竖直的半圆弧轨道BC在B处相连接,有-质量为2kg的滑块(可视为质点),在水平向右、大小为14N的恒力F作用下,从A点由静止开始运动到B点,滑块与AB间的动摩擦因数为μ=0.25,BC 间粗糙,取g=10m/s2.求: