题目内容
4.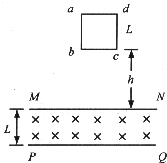 如图所示,在高度为L=1m、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B=1T.质量为m=1kg、边长为L=1m、总电阻R=1Ω的正方形导线框abcd(线框每条边的电阻相同),在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g取10m/s2,不计空气阻力,求:
如图所示,在高度为L=1m、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B=1T.质量为m=1kg、边长为L=1m、总电阻R=1Ω的正方形导线框abcd(线框每条边的电阻相同),在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g取10m/s2,不计空气阻力,求:(1)导线框刚下落时,bc边距磁场上边界MN的高度h;
(2)导线框刚进入磁场时bc边的电压Ubc;
(3)导线框穿越磁场的整个过程中,导线框中产生的热量Q.
分析 (1)线框速度达到稳定时,说明线框受力平衡即线框所受重力和安培力平衡,根据安培力的大小求出此时感应电流的大小,根据欧姆定律求出感应电动势从而求出此时线框的速度,根据动能定理可以求出bc边距磁场上边界MN的高度h;
(2)bc边的电压Ubc=$\frac{3}{4}$E;
(3)当线框速度已达稳定时,从能量守恒的角度分析处理,线框减少的重力势能等于线框增加的动能与产生的热量之和,计算出线框减少的势能再计算出产生的热量即可.
解答 解:设线框进入磁场时的速度为v,由于导线框恰好做匀速运动,所以安培力与重力大小相等,方向相反,
即mg=F安;
线框bc边切割磁感线产生的电动势为:E=BLv
故线框中产生的电流为:I=$\frac{E}{R}$
线框在磁场中所受安培力为:F安=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$
线框进入磁场前做自由落体运动,根据动能定理可以求出线框进入磁场时的速度v,即:
mgh=$\frac{1}{2}m{v}^{2}$-0
联立解得:h=$\frac{{m}^{2}g{R}^{2}}{2{B}^{4}{L}^{4}}$
(2)根据电路特点和欧姆定律知Ubc=$\frac{3}{4}$RI=$\frac{3}{4}$R$•\frac{mg}{BL}$=$\frac{3mgR}{4BL}$
(3)由于磁场的宽度与线框的宽度相等,所以线框匀速穿过整个的磁场,整个的过程中线框减小的重力势能转化为线框产生的热量,即:
Q=mg•2L
答:(1)导线框刚下落时,bc边距磁场上边界MN的高度是$\frac{{m}^{2}g{R}^{2}}{2{B}^{4}{L}^{4}}$;
(2)导线框刚进入磁场时bc边的电压Ubc为$\frac{3mgR}{4BL}$;
(3)导线框穿越磁场的整个过程中,导线框中产生的热量是2mgL.
点评 本题是电磁感应与力学知识的综合,安培力是联系电磁感应和力学的桥梁,安培力的分析和计算是这类问题的关键.

| A. | 只有a点 | B. | 只有c点 | C. | b点和c点 | D. | b点和a点 |
 如图所示,在x轴上方有垂直纸面向里的匀强磁场,磁感应强度大小为B,在原点O处有一粒子源,t=0时刻沿纸面内的各个方向同时发射一群速率相同、质量为m、电荷量为+q的粒子,其中一个与x轴正方向成60°角射入磁场的粒子在t1时刻到达A点(图中未画出),A点为该粒子运动过程中距离x轴的最远点,且OA=L.不计粒子间的相互作用和粒子的重力,下列结论正确的是( )
如图所示,在x轴上方有垂直纸面向里的匀强磁场,磁感应强度大小为B,在原点O处有一粒子源,t=0时刻沿纸面内的各个方向同时发射一群速率相同、质量为m、电荷量为+q的粒子,其中一个与x轴正方向成60°角射入磁场的粒子在t1时刻到达A点(图中未画出),A点为该粒子运动过程中距离x轴的最远点,且OA=L.不计粒子间的相互作用和粒子的重力,下列结论正确的是( )| A. | 粒子的速率为$\frac{qBL}{2m}$ | |
| B. | 粒子的速率为$\frac{\sqrt{3}qBL}{3m}$ | |
| C. | t1时刻仍在磁场中的所有粒子均处在以O点为圆心、L为半径的$\frac{1}{4}$圆周上 | |
| D. | t1时刻仍在磁场中的所有粒子均处在以O点为圆心、L为半径的$\frac{1}{3}$圆周上 |
| A. | 电子称所使用的测力装置是力传感器 | |
| B. | 电饭锅中的温度传感器其主要元件是感温铁氧体 | |
| C. | 话筒是一种常用的声音传感器,其作用是将电信号转化为声信号 | |
| D. | 干簧管可以起到开关作用,是一种能够感知磁场的传感器 |
 美国物理学家密立根(R•A•Millikan)在1907-1913年的七年间,致力于测量微小油滴上所带电荷的工作,这即是著名的密立根油滴实验,它是近代物理学发展过程中具有重要意义的实验.如图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴从上板中央小孔落入匀强电场中,空气阻力和浮力可忽略,通过显微镜可以观察到油滴的运动情况,根据上述实验,下列说法正确的是( )
美国物理学家密立根(R•A•Millikan)在1907-1913年的七年间,致力于测量微小油滴上所带电荷的工作,这即是著名的密立根油滴实验,它是近代物理学发展过程中具有重要意义的实验.如图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴从上板中央小孔落入匀强电场中,空气阻力和浮力可忽略,通过显微镜可以观察到油滴的运动情况,根据上述实验,下列说法正确的是( )| A. | 图中能刚好悬浮的油滴带的是正电荷 | |
| B. | 由qE=mg求油滴带的电荷量 | |
| C. | 通过该实验装置可直接测量出电子所带的电荷量 | |
| D. | 不同油滴所带电荷量虽不相同,但都是某个最小电荷量的整数倍 |
| A. | 汽车驶过拱形桥顶端 | |
| B. | 荡秋千的小孩通过最低点 | |
| C. | 跳水运动员被跳板弹起,离开跳板向上运动 | |
| D. | 宇宙飞船绕地球做匀速圆周运动 |
 2014年12月16日,国内普通居民住宅区首部“座椅式”电梯落户上海市某小区(如图).电梯由轨道及连接在其上的座椅组成.现有一体重为50kg的人从一楼乘坐至二楼,中间经过一水平拐弯处,可看做一段半径为1m的圆弧.已知座椅的质量为10kg,人与座椅间的动摩擦因数为0.5,座椅面水平,全程电梯速率保持不变,下列说法正确的是( )
2014年12月16日,国内普通居民住宅区首部“座椅式”电梯落户上海市某小区(如图).电梯由轨道及连接在其上的座椅组成.现有一体重为50kg的人从一楼乘坐至二楼,中间经过一水平拐弯处,可看做一段半径为1m的圆弧.已知座椅的质量为10kg,人与座椅间的动摩擦因数为0.5,座椅面水平,全程电梯速率保持不变,下列说法正确的是( )| A. | 拐弯时座椅和人做匀速圆周运动 | |
| B. | 椅子对人的作用力始终与人的重力平衡 | |
| C. | 若人在水平面上只受到座椅带来的摩擦力,为了使人不滑下座椅,拐弯时允许的最大速率为$\sqrt{5}$m/s | |
| D. | 若以最大速度拐弯,则轨道对椅子的作用力的大小为900N |
 如图所示,有一磁感强度B=0.1T的水平强磁场,垂直放置一很长的金属框架,框架上有一导体ab与框架边垂直且始终保持良好接触,由静止开始下滑,已知框架的宽度为1m,质量为0.1kg,电阻为0.1Ω,框架电阻不计,取g=10m/s2,求:
如图所示,有一磁感强度B=0.1T的水平强磁场,垂直放置一很长的金属框架,框架上有一导体ab与框架边垂直且始终保持良好接触,由静止开始下滑,已知框架的宽度为1m,质量为0.1kg,电阻为0.1Ω,框架电阻不计,取g=10m/s2,求: 如图所示,在半径为R的圆形区域内有水平向里的匀强磁场,圆形区域右侧距离圆形区域右边缘为d处有一竖直感光板.圆形区域上侧有两块平行金属极板,金属极板上侧有一粒子源,粒子源中可以发射速度很小的质量为m的2价阳离子(带电量为+2e),离子重力不计.
如图所示,在半径为R的圆形区域内有水平向里的匀强磁场,圆形区域右侧距离圆形区域右边缘为d处有一竖直感光板.圆形区域上侧有两块平行金属极板,金属极板上侧有一粒子源,粒子源中可以发射速度很小的质量为m的2价阳离子(带电量为+2e),离子重力不计.