题目内容
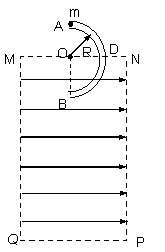
如图所示：矩形区域MNPQ内有水平向右的匀强电场，虚线框外为真空区域；半径为R、内壁光滑、内径很小的绝缘半圆管ADB固定在竖直平面内，直径AB垂直于水平虚线MN，圆心O为MN的中点，半圆管的一半处于电场中。一带正电的小球从半圆管的A点由静止开始滑入管内，小球可视为质点，质量为m，电量为q，当小球达到B点时，对管壁的压力为FN=3mg，重力加速度为g，求：
（1）匀强电场的电场强度E；
（2）若小球能从矩形框的右边界NP离开电场，矩形区域MNPQ的最小面积S.
(1)设小球从B点滑出时的速度为v0
小球过B点时： FN – mg= m
………………………………………………………………………………………2分
v0=
A到B，由动能定理有：2mgR– qER= 
mB v02………………………………………………………………2分
解得：E= 
………………………………………………………………………………………………………………………2分
(2)小球从B点滑出后，在水平方向做变速直线运动，竖直方向做自由落体运动
水平方向：ax = 
= g……………………………………………………………………………………………… 1分
竖直方向：ay = g ………………………………………………………………………………………………… 1分
设向左减速时间为t1，则有t1= 
= 
……………………………………………………………………… 1分
小球向左运动的最大距离：x = 
= R ………………………………………………………………………2分
虚线框MNPQ的最小宽度L=2R
设向左减速时间为t2，则有L = axt22
t2= 2
…………………………………………………………………… 1分
小球出电场时，下落的高度 h = ay(t1+t2)2 = (3+2
)R…………………………………………………………2分
虚线框MNPQ高度应满足 H>R+h
故虚线框MNPQ的最小面积S= HminL=4(2+)R 2………………………………………………………………2分
如图所示，矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场，在ad边中点O，向磁场区域射入一初速度方向垂直磁场且跟ad边夹角θ=30°的带正电粒子，已知粒子质量为m，电量为q，ad边长为L，ab边足够长，粒子重力不计．
如图所示，矩形区域MNPQ内有水平向右的匀强电场，虚线框外为真空区域；半径为R、内壁光滑、内径很小的绝缘半圆管ADB固定在竖直平面内，直径AB垂直于水平虚线MN，圆心O恰在MN的中点，半圆管的一半处于电场中．一质量为m，可视为质点的带正电电荷量为q的小球从半圆管的A点由静止开始滑入管内，小球从B点穿出后，能够通过B点正下方的C点．重力加速度为g，小球在C点处的加速度大小为5g/3．求：
如图所示，矩形区域MNPQ内有水平向右的匀强电场，虚线框外为真空区域，半径为R，内壁光滑，内径很小的绝缘半圆管ADB固定在竖直平面内，直径AB垂直于水平虚线MN，圆心O恰好在MN的中点，半圆管的一半处于电场中，一质量为m，可视为质点的带正电，电荷量为q的小球从半圆管的A点由静止开始滑入管内，小球从B点穿过后，能够通过B点正下方的C点，重力加速度为g，小球在C点处的加速度大小为
（2011?郑州模拟）如图所示，矩形区域MNPQ内有水平向右的匀强电场；在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小为B．半径为R的光滑绝缘空心半圆细管ADO固定在竖直平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN．一质量为m、电荷量为q的带正电小球（可视为质点）从圆管的A点由静止滑入管内，从O点穿出后恰好通过O点正下方的C点．已知重力加速度为g，电场强度的大小E=
如图所示，矩形区域MNPQ内有水平向右的匀强电场；在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小为B．半径为R的光滑绝缘空心半圆细管ADO固定在竖直平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN．一质量为m、电荷量为q的带正电小球（可视为质点）从半圆管的A点由静止滑入管内，从O点穿出后恰好通过O点正下方的C点．已知重力加速度为g，电场强度的大小