题目内容
11. 2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240m的山坡处泥石流以8m/s的初速度、0.4m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机的反应时间为1s,汽车启动后以0.5m/s2的加速度一直做匀加速直线运动.试分析汽车能否安全脱离?
2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240m的山坡处泥石流以8m/s的初速度、0.4m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机的反应时间为1s,汽车启动后以0.5m/s2的加速度一直做匀加速直线运动.试分析汽车能否安全脱离?
分析 根据匀变速直线运动的规律求得泥石流到达坡底的速度和时间,再根据脱离危险的临界条件求解是否可以脱离危险.
解答 解:设泥石流到达坡底的时间为t1,速率为v1,则由匀变速直线运动的规律有:
s1=v0t1+$\frac{1}{2}$a1t12
v1=v0+a1t1
代入数值得:t1=20s,v1=16m/s
而汽车在19s的时间内发生位移为:s2=$\frac{1}{2}$a2t22=$\frac{1}{2}×0.5×1{9}^{2}m$=90.25 m
速度为:v2=a2t2=0.5×19m/s=9.5 m/s
令再经时间t3,泥石流追上汽车,则有:
v1t3=s2+v2t3+$\frac{1}{2}$a2t32
代入数值并化简得:
t32-26t3+361=0,
由数学方程知,△<0,该方程无解.所以泥石流无法追上汽车,司机能安全脱离危险.
答:汽车能安全脱离危险.
点评 掌握匀变速直线运动的速度时间关系和位移时间关系能根据相遇条件列式求解,由数学关系确定是否安全脱离危险.

练习册系列答案
相关题目
19. 如图所示为物体在某段运动过程中的v-t图象,物体在t1和t2时刻的瞬时速度分别为v1和v2,则在时间t1到t2的过程中,下列判断正确的是( )
如图所示为物体在某段运动过程中的v-t图象,物体在t1和t2时刻的瞬时速度分别为v1和v2,则在时间t1到t2的过程中,下列判断正确的是( )
 如图所示为物体在某段运动过程中的v-t图象,物体在t1和t2时刻的瞬时速度分别为v1和v2,则在时间t1到t2的过程中,下列判断正确的是( )
如图所示为物体在某段运动过程中的v-t图象,物体在t1和t2时刻的瞬时速度分别为v1和v2,则在时间t1到t2的过程中,下列判断正确的是( )| A. | 物体的加速度不断增大 | B. | 物体的加速度不断减小 | ||
| C. | 物体的平均速度v=$\frac{{v}_{1}+{v}_{2}}{2}$ | D. | 物体的平均速度v>$\frac{{v}_{1}+{v}_{2}}{2}$ |
6.2008年9月25日至28日,我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,然后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
| A. | 飞船变轨前后的机械能相等 | |
| B. | 飞船在圆轨道上飞行时航天员出舱前后都处于失重状态 | |
| C. | 飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度 | |
| D. | 飞船变轨前通过椭圆轨道远地点时的向心加速度与变轨后沿圆轨道运动的向心加速度大小相等 |
16. 如图为一理想变压器,原、副线圈的匝数比为n.原线圈接正弦交流电压u=U0sinωt,输出端接有一个交流电流表和一个电动机.电动机的线圈电阻R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )
如图为一理想变压器,原、副线圈的匝数比为n.原线圈接正弦交流电压u=U0sinωt,输出端接有一个交流电流表和一个电动机.电动机的线圈电阻R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )
 如图为一理想变压器,原、副线圈的匝数比为n.原线圈接正弦交流电压u=U0sinωt,输出端接有一个交流电流表和一个电动机.电动机的线圈电阻R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )
如图为一理想变压器,原、副线圈的匝数比为n.原线圈接正弦交流电压u=U0sinωt,输出端接有一个交流电流表和一个电动机.电动机的线圈电阻R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )| A. | 原线圈中的电流为nI | |
| B. | 电动机两端的电压为IR | |
| C. | 电动机消耗的电功率为$\frac{{U}_{0}I}{\sqrt{2}n}$ | |
| D. | 重物匀速上升的速度为$\frac{I({U}_{0}-\sqrt{2}nIR)}{\sqrt{2}nmg}$ |

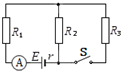 如图所示,电源电动势E=10V,内阻r=1Ω,R1=3Ω.电键S断开时,R2的功率为4W,电源的输出功率为4.75W,则电流表的读数为0.5A;电键S接通后,电流表的读数为2A.则R3=$\frac{16}{15}$Ω.
如图所示,电源电动势E=10V,内阻r=1Ω,R1=3Ω.电键S断开时,R2的功率为4W,电源的输出功率为4.75W,则电流表的读数为0.5A;电键S接通后,电流表的读数为2A.则R3=$\frac{16}{15}$Ω. 如图所示,ab、bd、cd是竖直平面内三根固定的细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为最低点.每根杆上都套着一个小滑环(图中末画出).三个滑环分别从a、b、c处释放(初速为0),用t1、t2、t3依次表示各滑环到达d点所用的时间,t1、t2、t3之间的关系为t1=t2=t3.
如图所示,ab、bd、cd是竖直平面内三根固定的细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为最低点.每根杆上都套着一个小滑环(图中末画出).三个滑环分别从a、b、c处释放(初速为0),用t1、t2、t3依次表示各滑环到达d点所用的时间,t1、t2、t3之间的关系为t1=t2=t3.
