题目内容
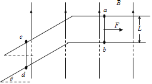
【题目】“翻滚过上车”的物理原理可以用如图所示装置演示。光滑斜槽轨道AD与半径为
的竖直圆轨道（圆心为O）相连，AD与圆O相切于D点，B为轨道的最低点，
。质量
的小球从距D点
处由静止开始下滑，然后冲上光滑的圆形轨道（取
，
，
）。求：
（1）求小球进入圆轨道B点时对轨道压力；
（2）计算分析小球能否通过竖直圆轨道的最高点C，并说明理由。
【答案】（1）17N，方向竖直向下（2）能过最高点C
【解析】
（1）小球由A至B，机械能守恒，则：mg（Lsin37°+hDB）=
其中：hDB=R（1-cos37°）
小球通过B点时：FN-mg=m
联立解得FN=17N
由牛顿第三定律可知，小球进入圆轨道B点时对轨道压力为17N，方向竖直向下；
（2）小球要过最高点，需要的最小速度为v0．则：mg=m
得：v0=
=1m/s
又小球从A到C机械能守恒，所以有 mg[Lsin37°-R（1+cos37°）]= 
解得 vC=
m/s＞1m/s，故小球能过最高点C．
练习册系列答案
相关题目
