题目内容
14.小木块从1m长,0.6m高的斜面顶端滑下,动摩擦因数是0.2,它滑到下端时的速度是多大?分析 木块沿斜面下滑,应用动能定理可以求出木块到达低端时的速度.
解答 解:对木块,由动能定理得:
mgh-μmgcosθ×L=$\frac{1}{2}$mv2-0,
由题意可知:cosθ=$\frac{\sqrt{{L}^{2}-{h}^{2}}}{L}$,
解得:v≈2.97m/s;
答:它滑到下端时的速度为2.97m/s.
点评 本题考查了求木块的速度,分析清楚木块运动过程、应用动能定理可以解题,本题也可以应用牛顿第二定律与运动学公式解题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
4.下列关于质点的说法,正确的是( )
| A. | 研究火车从南京到上海运行需要的时间,不能把火车看做质点 | |
| B. | 研究一辆汽车通过长江大桥所需的时间,不能把汽车看做质点 | |
| C. | 研究奥运会乒乓球运动员打出的弧圈球时,不能把乒乓球看做质点 | |
| D. | 研究奥运会跳水运动员的跳水动作时,不能把运动员看做质点 |
5.某同学在做探究弹力和弹簧伸长关系的实验中,设计了如图a所示的实验装置.所用钩码的单个质量都是30g,他先测出不挂钩码时弹簧的自然长度,然后再将4个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中:(弹力始终未超过弹性限度,取g=10m/s2)
①请根据表格中的实验数据,在给定的坐标纸 (图b) 上作出弹簧所受弹力F与弹簧伸长的长度x的F-x图线;

②由此可求出弹簧的劲度系数为24.0N/m.(计算结果保留三位有效数字).
| 钩码质量(g) | 0 | 30 | 60 | 90 | 120 |
| 弹簧总长(cm) | 6.00 | 7.25 | 8.48 | 9.78 | 11.04 |
| 弹力大小(N) | 0.0 | 0.3 | 0.6 | 0.9 | 1.2 |
| 弹簧伸长(cm) | 0.00 | 1.25 | 2.48 | 3.78 | 5.04 |

②由此可求出弹簧的劲度系数为24.0N/m.(计算结果保留三位有效数字).
2.电磁打点计时器的工作电压是及电流( )
| A. | 220v 交流电 | B. | 220v 直流电 | C. | 6v以下 交流电 | D. | 6v以下 直流电 |
4.一航天飞机下有一细金属杆,杆指向地心.若仅考虑地磁场的影响,则当航天飞机位于赤道上空( )
| A. | 由东向西水平飞行时,金属杆中感应电动势的方向一定由上向下 | |
| B. | 由西向东水平飞行时,金属杆中感应电动势的方向一定由上向下 | |
| C. | 沿地磁极的经线由南向北水平飞行时,金属杆中感应电动势的方向一定由下向上 | |
| D. | 沿地磁极的经线由北向南水平飞行时,金属杆中感应电动势的方向一定由上向下 |
11. 如图,理想变压器原、副线圈分别接有额定电压相同的灯泡a和b.当输入电压U为灯泡额定电压的9倍时,两灯泡均能正常发光.下列说法正确的是( )
如图,理想变压器原、副线圈分别接有额定电压相同的灯泡a和b.当输入电压U为灯泡额定电压的9倍时,两灯泡均能正常发光.下列说法正确的是( )
 如图,理想变压器原、副线圈分别接有额定电压相同的灯泡a和b.当输入电压U为灯泡额定电压的9倍时,两灯泡均能正常发光.下列说法正确的是( )
如图,理想变压器原、副线圈分别接有额定电压相同的灯泡a和b.当输入电压U为灯泡额定电压的9倍时,两灯泡均能正常发光.下列说法正确的是( )| A. | 此时a和b的电流之比为1:1 | B. | 原、副线圈匝数之比为9:1 | ||
| C. | 原、副线圈匝数之比为8:1 | D. | 此时a和b的电功率之比为8:1 |
8. 如图所示,在光滑水平面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示,PQ为两个磁场的边界,磁场范围足够大.一个共n匝,边长为a,总质量为m,总电阻为R的正方形金属线框垂直磁场方向,以速度v从图示位置向右运动,当线框中心线AB运动到PQ重合时,线框的速度为$\frac{v}{3}$,则( )
如图所示,在光滑水平面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示,PQ为两个磁场的边界,磁场范围足够大.一个共n匝,边长为a,总质量为m,总电阻为R的正方形金属线框垂直磁场方向,以速度v从图示位置向右运动,当线框中心线AB运动到PQ重合时,线框的速度为$\frac{v}{3}$,则( )
 如图所示,在光滑水平面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示,PQ为两个磁场的边界,磁场范围足够大.一个共n匝,边长为a,总质量为m,总电阻为R的正方形金属线框垂直磁场方向,以速度v从图示位置向右运动,当线框中心线AB运动到PQ重合时,线框的速度为$\frac{v}{3}$,则( )
如图所示,在光滑水平面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示,PQ为两个磁场的边界,磁场范围足够大.一个共n匝,边长为a,总质量为m,总电阻为R的正方形金属线框垂直磁场方向,以速度v从图示位置向右运动,当线框中心线AB运动到PQ重合时,线框的速度为$\frac{v}{3}$,则( )| A. | 此时线框中的电功率为$\frac{{4{n^2}{B^2}{a^2}{v^2}}}{9R}$ | |
| B. | 此时线框的加速度为$\frac{{4{n^2}{B^2}{a^2}v}}{3R}$ | |
| C. | 此过程通过线框截面的电量为$\frac{{B{a^2}}}{R}$ | |
| D. | 此过程回路产生的电能为$\frac{1}{6}m{v^2}$ |
9.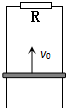 如图所示,在竖直平面内的两根平行金属导轨,顶端用一电阻R相连,磁感应强度为B的匀强磁场垂直导轨平面.一质量为m的金属棒他们ab以初速度v0沿导轨竖直向上运动,到某一高度后又返回下行到原处,整个过程金属棒与导轨接触良好,导轨与棒的电阻不计.则在上行与下行两个过程中,下列说法正确的是( )
如图所示,在竖直平面内的两根平行金属导轨,顶端用一电阻R相连,磁感应强度为B的匀强磁场垂直导轨平面.一质量为m的金属棒他们ab以初速度v0沿导轨竖直向上运动,到某一高度后又返回下行到原处,整个过程金属棒与导轨接触良好,导轨与棒的电阻不计.则在上行与下行两个过程中,下列说法正确的是( )
 如图所示,在竖直平面内的两根平行金属导轨,顶端用一电阻R相连,磁感应强度为B的匀强磁场垂直导轨平面.一质量为m的金属棒他们ab以初速度v0沿导轨竖直向上运动,到某一高度后又返回下行到原处,整个过程金属棒与导轨接触良好,导轨与棒的电阻不计.则在上行与下行两个过程中,下列说法正确的是( )
如图所示,在竖直平面内的两根平行金属导轨,顶端用一电阻R相连,磁感应强度为B的匀强磁场垂直导轨平面.一质量为m的金属棒他们ab以初速度v0沿导轨竖直向上运动,到某一高度后又返回下行到原处,整个过程金属棒与导轨接触良好,导轨与棒的电阻不计.则在上行与下行两个过程中,下列说法正确的是( )| A. | 通过R的电荷量相等 | B. | 回到出发点的速度v等于初速度v0 | ||
| C. | 电阻R上产生的热量相等 | D. | 所用时间相等 |
