题目内容
10. 如图所示,用细圆管组成的光滑轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r<<R.有一质量为m,半径比r略小的光滑小球以水平初速度v0射入圆管.
如图所示,用细圆管组成的光滑轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r<<R.有一质量为m,半径比r略小的光滑小球以水平初速度v0射入圆管.若要小球能从C端出来,初速度v0需多大?
分析 当球恰好能从C端出来时,速度为零,机械能守恒,可以直接用动能定理求解初速度v0.
解答 解:当球恰好能从C端出来时,速度vC=0.
根据动能定理得:-mg•2R=0-$\frac{1}{2}m{v}_{0}^{2}$,
解得:${v}_{0}=2\sqrt{gR}$
所以要使小球能从C端出来,初速度v0≥$2\sqrt{gR}$.
答:要使小球能从C端出来,初速度v0≥$2\sqrt{gR}$.
点评 在运动的过程中只有重力做功,可以直接用动能定理计算初速度的大小,这样比较简单,难度不大.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 液晶具有流动性,光学性质各向异性 | |
| B. | 气体扩散现象表明气体分子间存在斥力 | |
| C. | 热量总是自发的从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 机械能不可能全部转化为内能,内能也无法全部用来做功以转化成机械能 |
1.船在静水中的速度是4m/s,河岸笔直,河宽40m,河水流速为3m/s,以下说法正确的是( )
| A. | 船过河的位移可能为30m | B. | 船在河中运动速度一定为5 m/s | ||
| C. | 船可以垂直过河 | D. | 船过河的时间可能为8s |
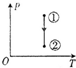
 如图所示,内壁光滑的导热气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸中.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②.如果环境保持恒温,则下图中可表示此过程的图象是( )
如图所示,内壁光滑的导热气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸中.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②.如果环境保持恒温,则下图中可表示此过程的图象是( )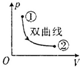


 如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.
如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2. 水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行安全检查.如图所示为一水平传送带装置示意图,绷紧的传送带AB始终保持v=4m/s的恒定速率运行,一质量为m=4kg的行李无初速地放在A处,设行李与传送带间的动摩擦因数μ=0.1,AB间的距离L=2m,g取10m/s2.
水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行安全检查.如图所示为一水平传送带装置示意图,绷紧的传送带AB始终保持v=4m/s的恒定速率运行,一质量为m=4kg的行李无初速地放在A处,设行李与传送带间的动摩擦因数μ=0.1,AB间的距离L=2m,g取10m/s2.