题目内容
10.如图所示,在坐标系xoy平面内有一半径为a的圆形区域,圆心坐标O1(a,0)圆内分布有垂直于纸面向里的匀强磁场.在直线y=a的上方和直线x=2a的左侧区域内,有一沿x轴正向的匀强电场,场强为E.在x=2a处有一平行于y轴的足够大荧光屏.在O点有一个粒子源,能在第一象限向各个方向垂直磁场发射出质量为m、电荷量为+q、速度大小为v的相同粒子.其中沿x轴正方向的一粒子,恰好能从O1点的正上方的A点射出磁场.不计粒子的重力.
(1)求磁感应强度B的大小;
(2)求所有射出的粒子打在荧光屏上的范围;
(3)若撤去荧光屏,保持电场大小不变,方向改为沿y轴负方向.求沿x轴正方向成θ=30°射入磁场的粒子在电场中能到达最远的位置坐标及最后射出磁场的位置坐标.
分析 (1)根据几何关系求出粒子在磁场中运动的半径,结合半径公式求出磁感应强度的大小.
(2)从O点射出的沿x轴正向的粒子打在屏上最低点,从O点沿y轴正向射出的粒子打在屏上最高点,根据类平抛运动的规律求出所有射出的粒子打在荧光屏上的范围.
(3)作出粒子的运动轨迹,结合几何关系和动能定理求出在电场中最远坐标,根据几何关系求出最后射出磁场的位置坐标.
解答 解:(1)设粒子在磁场中做圆运动的轨迹半径为R,根据牛顿第二定律,有$qvB=m\frac{{v}^{2}}{R}$,
沿x轴正方向的一粒子,恰好能从O1点的正上方的A点射出磁场,根据几何关系知,R=a,
解得B=$\frac{mv}{qa}$.
(2)从O点射出的沿x轴正向的粒子打在屏上最低点,
$a=\frac{qE}{2m}{{t}_{1}}^{2}$,${t}_{1}=\sqrt{\frac{2ma}{qE}}$,
${y}_{1}=a+v{t}_{1}=a+v\sqrt{\frac{2ma}{qE}}$.
从O点沿y轴正向射出的粒子打在屏上最高点,
$2a=\frac{qE}{2m}{{t}_{2}}^{2}$,${t}_{2}=\sqrt{\frac{4ma}{qE}}$.
${y}_{2}=a+v{t}_{2}=a+v\sqrt{\frac{4ma}{qE}}$,
所以粒子打在荧光屏上的范围为$a+v\sqrt{\frac{2ma}{qE}}≤y≤a+v\sqrt{\frac{4ma}{qE}}$.
(3)粒子在磁场中做匀速圆周运动,出磁场时:
$x=r-rcos60°=\frac{a}{2}$,
粒子进电场后做匀减速运动,上升阶段有:
$\frac{1}{2}m{v}^{2}=qE△y$,
$△y=\frac{m{v}^{2}}{2qE}$,
所以在电场中最远坐标为$(\frac{a}{2},a+\frac{m{v}^{2}}{2qE})$,
因为粒子的轨迹半径与磁场的边界半径相等,粒子返回磁场后射入点和射出点与轨迹圆心及磁场的边界圆心的连线构成菱形,所以最后射出磁场的坐标为(2a,0),
答:(1)磁感应强度B的大小为$\frac{mv}{qa}$;
(2)所有射出的粒子打在荧光屏上的范围为$a+v\sqrt{\frac{2ma}{qE}}≤y≤a+v\sqrt{\frac{4ma}{qE}}$;
(3)沿x轴正方向成θ=30°射入磁场的粒子在电场中能到达最远的位置坐标为$(\frac{a}{2},a+\frac{m{v}^{2}}{2qE})$,最后射出磁场的位置坐标为(2a,0).
点评 本题关键先确定圆心、半径,然后根据洛伦兹力提供向心力列式求解;第二问确定两个临界状态,结合类平抛运动的规律进行求解.第三问关键分析后画出物体的运动轨迹,然后再列式计算.

 习题精选系列答案
习题精选系列答案 2013年12月2日,“长征三号乙”运载火箭将“嫦娥三号”月球探测器成功送入太空,12月6日“嫦娥三号”由地月转移轨道进入100公里环月轨道,12月10日成功变轨到近月点为15公里的椭圆轨道,12月14日从15公里高度降至月球表面成功实现登月.则关于“嫦娥三号”登月过程的说法正确的是( )
2013年12月2日,“长征三号乙”运载火箭将“嫦娥三号”月球探测器成功送入太空,12月6日“嫦娥三号”由地月转移轨道进入100公里环月轨道,12月10日成功变轨到近月点为15公里的椭圆轨道,12月14日从15公里高度降至月球表面成功实现登月.则关于“嫦娥三号”登月过程的说法正确的是( )| A. | “嫦娥三号”由地月转移轨道需要减速才能进入100公里环月轨道 | |
| B. | “嫦娥三号”在近月点为15公里的椭圆轨道上各点的加速度都大于其在100公里圆轨道上的加速度 | |
| C. | “嫦娥三号”在100公里圆轨道上运动的周期大于其在近月点为15公里的椭圆轨道上运动的周期 | |
| D. | 从15公里高度降至月球表面过程中,“嫦娥三号”处于超重状态 |
 如图所示,MN,PQ是水平面内的两条光滑金属导轨,其电阻不计,金属棒ab垂直放置在两导轨上,匀强磁场垂直导轨平面.将ab棒由图示位置分别以速度v1和v2匀速拉到a′b′位置,比较这两个过程,下列说法正确的是( )
如图所示,MN,PQ是水平面内的两条光滑金属导轨,其电阻不计,金属棒ab垂直放置在两导轨上,匀强磁场垂直导轨平面.将ab棒由图示位置分别以速度v1和v2匀速拉到a′b′位置,比较这两个过程,下列说法正确的是( )| A. | 若v1>v2,两次通过棒a,b截面的电量关系是q1>q2 | |
| B. | 若v1>v2,两次拉力关系是F1>F2 | |
| C. | 若v1>2v2,两次拉力做功关系是W1=W2 |
| A. | 只要知道气体的摩尔体积和阿伏伽德罗常数,就可以算出气体分子的体积 | |
| B. | 在同一温度下,悬浮在液体中的固体微粒越小,布朗运动就越明显 | |
| C. | 一定温度下,饱和汽的压强是一定的 | |
| D. | 第二类永动机不可能制成是因为它违反了能量守恒定律 | |
| E. | 由于液体表面分子间距离大于液体内部分子间的距离,液面分子间的引力大于斥力,所以液体表面具有收缩的趋势 |
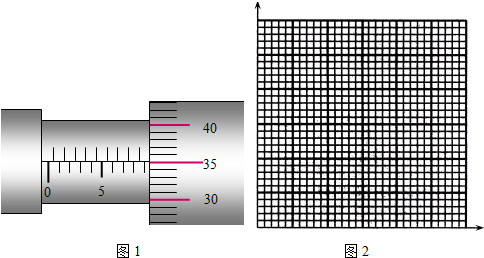
(1)首先用螺旋测微器测量小球的直径.如图1所示,则小球直径d=0.9350cm.
(2)让小球从凹槽上某位置由静止释放,并通过光电门.用刻度尺测量小球释放位置到光电门的距离x,光电门自动记录小球通过光电门的时间△t,可计算小球通过光电门的瞬时速度表达式为v=$\frac{d}{△t}$.(小球直径用d表示)
(3)改变小球的释放位置重复(2),可得到多组距离x、速度v.现将多组x、v、v2对应记录在表格中.
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 距离x/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| 速度v/ms-1 | 1.00 | 1.42 | 1.73 | 2.01 | 2.32 | 2.44 |
| 速度的平方v2/(m•s-1)2 | 1.00 | 2.02 | 2.99 | 4.04 | 5.38 | 5.95 |
(5)根据所作图象求得小球运动的加速度a=5.0m/s2(保留两位小数).
| A. | -Aωsinφ | B. | Aωsinφ | C. | -Aωcosφ | D. | Aωcosφ |

 在竖直平面内的空间中有一固定的“?”型绝缘细杆,ab杆和cd杆水平放置,杆长都为2R,c、b两点在同一竖直线上,其右侧平滑连接了一个半径为R的半圆形细杆,在ac、bd连线的交点O处固定了一个电量为Q的点电荷,另有与Q点电荷电性相同的质量为m,电量为q的带电圆环套在细杆的a端,若给带电圆环一水平向右的初速度,之后圆环在细杆上滑行,最后恰好能到达cd杆的d端,已知带电圆环与水平细杆之间的动摩擦因数为μ,带电圆环与半圆形细杆之间的摩擦可忽略不计,静电力常数为k,且mg>k$\frac{Qq}{{R}^{2}}$,重力加速度为g,求:
在竖直平面内的空间中有一固定的“?”型绝缘细杆,ab杆和cd杆水平放置,杆长都为2R,c、b两点在同一竖直线上,其右侧平滑连接了一个半径为R的半圆形细杆,在ac、bd连线的交点O处固定了一个电量为Q的点电荷,另有与Q点电荷电性相同的质量为m,电量为q的带电圆环套在细杆的a端,若给带电圆环一水平向右的初速度,之后圆环在细杆上滑行,最后恰好能到达cd杆的d端,已知带电圆环与水平细杆之间的动摩擦因数为μ,带电圆环与半圆形细杆之间的摩擦可忽略不计,静电力常数为k,且mg>k$\frac{Qq}{{R}^{2}}$,重力加速度为g,求: