题目内容

6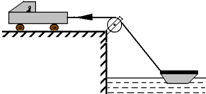．如图所示，汽车在河岸上通过细绳拖船靠岸，绕过滑轮的两段绳子在同一个竖直平面内，滑轮可视为质点，如果汽车牵引绳子匀速前进，则被拖的船将做（　　）
A．匀速运动B．加速运动
C．减速运动D．无法确定是加速还是减速的运动

分析 将小船的运动沿绳子收缩方向和垂直绳子方向进行正交分解，汽车拉绳子的速度v等于船沿绳子收缩方向的分速度，再结合沿绳子收缩方向的分速度，及三角知识，即可求解．

解答 解：如图所示，v车=v∥=v船cosθ，随着船的靠岸，θ越来越大，v船越来越大，即被拖的船将做加速运动，故B正确，ACD错误．
故选：B．

点评 本题关键是找出小船的两个分运动，然后将合速度分解，求出合速度与拉绳子速度的表达式，再进行讨论．

练习册系列答案
相关题目
16．游乐场中有一类似于过山车的设施．简易模型如图所示，它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成，A、B分别是斜面与圆形轨道的最低点（且A处有一极小光滑圆弧与轨道相切），A、B两点相距L=4.25m．一个质量为m=0.1kg的小球（视为质点），从斜面上距A点h=4.05m高处由静止下滑，小球与水平轨道的动摩擦因数μ=0.2．假设水平轨道足够长，不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响，sin37°=0.6，g取lOm/s2．求：
（1）若圆形轨道的半径R=l.0m，则小球到达B点时的速度大小及对轨道的压力大小：
（2）欲使小球不脱离轨道，在圆形轨道的设计中，半径应满足的条件和小球最终停留点与B点的距离．
17．${\;}_{27}^{60}$Co发生一次β衰变后变为Ni核，在该衰变过程中还发出频率为ν1和ν2的两个光子，试写出衰变方程式，并求出该核反应因释放光子而造成的质量亏损．
14．关于静电现象，下列说法正确的是（　　）
A．处于静电平衡的导体，内部电势处处为零
B．处于静电平衡的导体，其外表面场强大小处处相等
C．利用尖端放电的原理，避雷针可以有效的避免建筑物遭受雷击破坏
D．油罐车尾部装有一条拖地的铁链，是为了把罐体上的静电及时导入大地，从而避免了火花放电
1．下列说法正确的是（　　）
A．α粒子散射实验可以用来确定原子核电荷量和估算原子核半径
B．康普顿效应和电子的衍射现象说明粒子的波动性
C．氢原子辐射出一个光子后能量减小，核外电子运动的加速度增大
D．结合能越大，表示原子核中核子结合得越牢靠，原子核越稳定
11．图甲是科大著名服务机器人“可佳”，图乙是其处于水平面上要执行一项任务的运动轨道，其中A、B是长为3.0m的直导轨，B、C是半径为1m的四分之一圆弧轨道，C、D是长为2.0m的直导轨．执行任务时，“可佳”从A出发，先做匀加速运动，经过1.2s速度达到1.5m/s时开始做匀速率运动，到达D点前以大小是2倍于加速运动的加速度减速，到D点时恰好停止，则机器人“可佳”（　　）
A．在该次运动的整个过程中路程为7m
B．在该次运动的整个过程中位移大小为（3$\sqrt{2}$+1）m
C．在该次运动的整个过程中运动时间为$\frac{29+2π}{6}$s
D．在圆弧轨道上运动的速度变化率为2.25m/s2
18．下列说法中正确的是（　　）
A．在光发生折射现象时，折射角不一定小于入射角
B．某介质的折射率与入射角的正弦值成正比，与折射角的正弦值成反比
C．在光发生折射现象时，入射角增大到原来的2倍，折射角也增大到原来的2倍
D．当光以60°的入射角从介质a到另一种介质b时，折射角为45°；那么当光以45°的入射角从介质a到另介质b时，折射角为30°
15．如图所示，在“3•11”日本大地震的一次抢险救灾工作中，一架沿水平直线飞行的直升机利用降落伞匀速向下向灾区群众投放救灾物资．假设物资的总重量为G1，圆顶形降落伞伞面的重量为G2，有8条相同的拉线与物资相连，另一端均匀分布在伞的边缘上，每根拉线和竖直方向都成30°角，则每根拉线上的张力大小为（　　）
A．$\frac{\sqrt{3}{G}_{1}}{12}$B．$\frac{\sqrt{3}（{G}_{1}+{G}_{2}）}{12}$C．$\frac{{G}_{1}+{G}_{2}}{8}$D．$\frac{{G}_{1}}{4}$
16．如图所示，一束复色光L沿半径方向射入半圆形玻璃砖，a、b是复色光射入玻璃砖后经过一次折射后的其中两条出射单色光．玻璃砖对a光的折射率＞（填“＜”“=”“＞”）对b光的折射率．用同一双缝干涉仪做光的双缝干涉实验，a光条纹间距＜（填“＜”“=”“＞”）b光的条纹间距．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网