题目内容
12.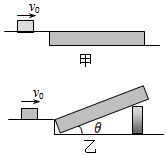 如图甲所示,光滑平台右侧与一长为L=2.5m的水平木板相接,木板固定在地面上,现有一小滑块以初速度v0=5m/s滑上木板,恰好滑到木板右端停止.现让木板右端抬高,如图乙所示,使木板与水平地面的夹角θ=37°,让滑块以相同的初速度滑上木板,不计滑块滑上木板时的能量损失,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图甲所示,光滑平台右侧与一长为L=2.5m的水平木板相接,木板固定在地面上,现有一小滑块以初速度v0=5m/s滑上木板,恰好滑到木板右端停止.现让木板右端抬高,如图乙所示,使木板与水平地面的夹角θ=37°,让滑块以相同的初速度滑上木板,不计滑块滑上木板时的能量损失,g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)滑块与木板之间的动摩擦因数μ;
(2)滑块从滑上倾斜木板到滑回木板底端所用的时间t.
分析 (1)根据速度位移公式求得加速度,利用牛顿第二定律求得摩擦因数;
(2)根据牛顿第二定律求得减速上滑和加速下滑的加速度,利用运动学公式求得减速上滑和加速下滑的时间即可求得
解答 解:(1)设滑块质量为m,木板水平时滑块加速度为a,则对滑块有
μmg=ma…①
滑块恰好到木板右端停止
$0{-v}_{0}^{2}=-2aL$…②
解得 $μ=\frac{{v}_{0}^{2}}{2gL}$=0.5…③
(2)当木板倾斜,设滑块上滑时的加速度为a1,最大距离为s,上滑的时间为t1,有
μmgcosθ+mgsinθ=ma1…④
${v}_{0}^{2}=-2{a}_{1}s$…⑤
0-v0-a1t1…⑥
由 ④⑤⑥式,解得 t1=0.5s…⑦
设滑块下滑时的加速度为a2,下滑的时间为t2,有
mgsinθ-μmgcosθ=ma2…⑧
$s=\frac{1}{2}{{a}_{2}t}_{2}^{2}$ …⑨
由⑧⑨式解得${t}_{2}=\frac{\sqrt{5}}{2}$s…⑩
滑块从滑上倾斜木板到滑回木板底端所用的时间
$t={t}_{1}+{t}_{2}=\frac{1+\sqrt{5}}{2}s$…⑪
答:(1)滑块与木板之间的动摩擦因数μ为0.5;
(2)滑块从滑上倾斜木板到滑回木板底端所用的时间t为t为$\frac{1+\sqrt{5}}{2}s$
点评 本题主要考查了牛顿第二定律和运动学公式,加速度是中间桥梁,关键是明确运动过程即可求得

练习册系列答案
相关题目
2.如图甲所示,定值电阻R1=3Ω,R2=2Ω,滑动变阻器RP的最大电阻为10Ω,电表均视为理想电表,调节RP记录多组U,I数据,画出了如图乙所示的U一I,图象,下列说法正确的是( )


| A. | 当滑动变阻器由中点向右移动时,滑动变阻器上的功率先增加后减小 | |
| B. | 当滑动变阻器的电阻为10Ω时,滑动变阻器的功率最大 | |
| C. | 当滑动变阻器的电阻为4Ω时,电源的效率最大 | |
| D. | 电源的最大功率为2.25 W |
3.下列关于热学规律的说法中正确的是( )
| A. | 温度低的物体内能小 | |
| B. | 物体吸收热量,其温度一定升高 | |
| C. | 自然界中自发进行的与热现象有关的宏观物理过程都具有方向性 | |
| D. | 悬浮在液体中的固体颗粒越大,周围液体分子撞击的机会越多,布朗运动越明显 |
20.一质点在做匀加速直线运动,加速度为a,在时间t内速度变为原来的3倍,则该质点在时间t内的位移为( )
| A. | $\frac{1}{2}$at2 | B. | at2 | C. | $\frac{3}{2}$at2 | D. | 2at2 |
9.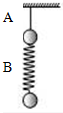 如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
 如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )| A. | aA=0,aB=g | B. | aA=g,aB=0 | C. | aA=0,aB=2g | D. | aA=2g,aB=0 |
 如图所示,一个质量为5kg的光滑球放在质量为20kg的小车中,小车顶板AB与底板CD间的距离恰好与小球直径相等,侧壁AD与顶板的夹角为45°,整个装置放在光滑水平面上,现对小车施加F=500N的水平拉力.求
如图所示,一个质量为5kg的光滑球放在质量为20kg的小车中,小车顶板AB与底板CD间的距离恰好与小球直径相等,侧壁AD与顶板的夹角为45°,整个装置放在光滑水平面上,现对小车施加F=500N的水平拉力.求