题目内容
15.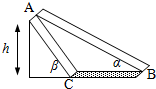 如图所示,用光滑材料制成高h=0.8m、倾角分别为α=30°和β=53°的两个斜面AB、AC,固定在光滑水平面上.将两个质量均为0.1kg的相同的小物块分别从两个斜面的最高位置A同时静止释放(不考虑一个物块在C点的能量损失),物块在BC上运动时给物块一个水平向左的阻力F,使两个物块同时到达B点.若g取10m/s2,sin53°=0.8.求:
如图所示,用光滑材料制成高h=0.8m、倾角分别为α=30°和β=53°的两个斜面AB、AC,固定在光滑水平面上.将两个质量均为0.1kg的相同的小物块分别从两个斜面的最高位置A同时静止释放(不考虑一个物块在C点的能量损失),物块在BC上运动时给物块一个水平向左的阻力F,使两个物块同时到达B点.若g取10m/s2,sin53°=0.8.求:(1)物块在BC上运动的时间t为多少?
(2)F为多少?
分析 根据几何关系求出AB、AC、CB的长度,根据牛顿第二定律求出AB、AC段的加速度大小,结合位移时间公式求出AB和AC段的时间,抓住运动的总时间相等,求出物块在BC上的运动时间.
根据速度位移公式求出C点的速度,结合位移时间公式求出BC段的加速度,通过牛顿第二定律求出阻力的大小.
解答 解:(1)AB得长度${l_{AB}}=\frac{h}{{sin{{30}^0}}}=\frac{0.8}{0.5}=1.6$m
AC的长度${l_{AC}}=\frac{h}{{sin{{53}^0}}}=\frac{0.8}{0.8}=1$m
CB段的长度${l}_{CB}=\frac{h}{tan30°}-\frac{h}{tan53°}=\frac{0.8}{\frac{\sqrt{3}}{3}}-\frac{0.8}{\frac{4}{3}}$≈0.79m.
根据牛顿第二定律得,AB段的加速度${a}_{AB}=gsin30°=10×\frac{1}{2}m/{s}^{2}=5m/{s}^{2}$,
AC段的加速度${a}_{AC}=gsin53°=10×0.8m/{s}^{2}$=8m/s2.
则AB段的时间${t_{AB}}=\sqrt{\frac{{2{l_{AB}}}}{{{a_{AB}}}}}=\sqrt{\frac{2×1.6}{5}}=0.8$s
AC段的时间${t_{AC}}=\sqrt{\frac{{2{l_{AC}}}}{{{a_{AC}}}}}=\sqrt{\frac{2×1}{8}}=0.5$s
t=tAB-tAC=0.8-0.5=0.3s
(2)C点的速度${v_C}=\sqrt{2gh}=\sqrt{2×10×0.8}=4$m/s
根据位移时间公式得,${l_{CB}}={v_C}t-\frac{1}{2}{a_{CB}}{t^2}$
$0.79=4×0.3-\frac{1}{2}×{a_{CB}}×{0.3^2}$
解得aCB≈9.1m/s2
根据牛顿第二定律得,F=maCB=0.1×9.1≈0.91N
答:(1)物块在BC上运动的时间t为0.3s.
(2)F为0.91N.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,抓住总时间相等,结合牛顿第二定律和运动学公式进行求解.

 名校课堂系列答案
名校课堂系列答案| A. | 该行星的半径为$\frac{vT}{2π}$ | B. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | ||
| C. | 无法测出该行星的质量 | D. | 该行星表面的重力加速度为$\frac{2πv}{T}$ |
| A. |  | B. |  | C. |  | D. |  |
 一列简谐横波沿x轴正向传播,传到M点时波形如图所示,再经0.6s,N点开始振动,则该波的振幅A为0.5m,周期T为0.4s.
一列简谐横波沿x轴正向传播,传到M点时波形如图所示,再经0.6s,N点开始振动,则该波的振幅A为0.5m,周期T为0.4s.



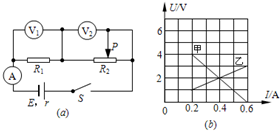 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合开关S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示.则电源内阻的阻值为5Ω,滑动变阻器R2的最大功率为0.9W.
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合开关S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示.则电源内阻的阻值为5Ω,滑动变阻器R2的最大功率为0.9W.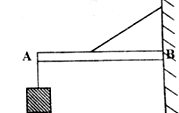 如图,均匀杆AB长1m,所受重力为G1,A端挂重物所受重力为G2.CD为一根轻绳,长也为1m,问要使AB杆保持水平位置,绳上的最小拉力为多少?
如图,均匀杆AB长1m,所受重力为G1,A端挂重物所受重力为G2.CD为一根轻绳,长也为1m,问要使AB杆保持水平位置,绳上的最小拉力为多少?


