题目内容
12.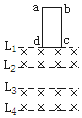 如图所示,在竖直纸面内有四条间距均为L的水平虚线L1、L2、L3、L4,在L1、L2之间与L3、L4之间存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场.现有一矩形线圈abcd,长边ad=3L,宽边cd=L,质量为m,电阻为R,将其从图示位置(cd边与L1重合)由静止释放,cd边经过磁场边界线L3时恰好开始做匀速直线运动,整个运动过程中线圈始终处于同一竖直平面内,cd边始终水平,已知重力加速度g=10m/s2,则( )
如图所示,在竖直纸面内有四条间距均为L的水平虚线L1、L2、L3、L4,在L1、L2之间与L3、L4之间存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场.现有一矩形线圈abcd,长边ad=3L,宽边cd=L,质量为m,电阻为R,将其从图示位置(cd边与L1重合)由静止释放,cd边经过磁场边界线L3时恰好开始做匀速直线运动,整个运动过程中线圈始终处于同一竖直平面内,cd边始终水平,已知重力加速度g=10m/s2,则( )| A. | ab边经过磁场边界线L1后线圈要做一段减速运动 | |
| B. | ab边经过磁场边界线L3后线圈要做一段减速运动 | |
| C. | cd边经过磁场边界线L2和L4的时间间隔为$\frac{2{B}^{2}{L}^{3}}{mgR}$ | |
| D. | 从线圈开始运动到cd边经过磁场边界线L4过程中,线圈产生的热量为3mgL-$\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$ |
分析 cd边经过磁场边界线L3时恰好做匀速直线运动,线圈所受的安培力和重力平衡,根据平衡条件求出匀速直线运动的速度.cd边从L2到L3的过程中,穿过线圈的磁通量没有改变,没有感应电流产生,不受安培力,线圈做匀加速直线运动,加速度为g,根据运动学公式求出此过程的时间,再求解线圈下面磁场的时间,即可求解线圈cd边经过磁场边界线L2和L4的时间间隔.根据能量守恒求出线圈中所产生的热量.
解答 解:A、cd边经过磁场边界线L3时恰好开始做匀速直线运动,cd边从L2到L3的过程中,穿过线圈的磁通量没有改变,没有感应电流产生,不受安培力,线圈做匀加速直线运动,可知,ab边经过磁场边界线L1后线圈要做一段减速运动,故A正确.
B、ab边从L2到L3的过程中,穿过线圈的磁通量没有改变,没有感应电流产生,不受安培力,线圈做匀加速直线运动,则ab边进入下方磁场的速度比cd边进入下方磁场的速度大,所受的安培力增大,所以ab边经过磁场边界线L3后线圈要做一段减速运动.故B正确.
C、cd边经过磁场边界线L3时恰好做匀速直线运动,根据平衡条件有:mg=BIL
而I=$\frac{BLv}{R}$
联立两式解得:v=$\frac{mgR}{{B}^{2}{L}^{2}}$
cd边从L3到L4的过程做匀速运动,所用时间为 t2=$\frac{L}{v}$=$\frac{{B}^{2}{L}^{3}}{mgR}$.
cd边从L2到L3的过程中线圈做匀加速直线运动,加速度为g,设此过程的时间为t1.
由运动学公式得:L=$\frac{{v}_{0}+v}{2}$t1<$\frac{2v}{2}{t}_{1}$=vt1,得 t1>$\frac{L}{v}$=$\frac{{B}^{2}{L}^{3}}{mgR}$.
故cd边经过磁场边界线L2和L4的时间间隔为 t=t1+t2>2$\frac{L}{v}$=$\frac{2{B}^{2}{L}^{3}}{mgR}$.故C错误.
D、线圈从开始运动到cd边经过磁场边界线L4过程,根据能量守恒得:Q=mg•3L-$\frac{1}{2}$mv2=3mgL-$\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$.故D正确.
故选:ABD
点评 解决本题的关键理清线圈的运动情况,选择合适的规律进行求解,分别从力和能量两个角度进行研究.

 阅读快车系列答案
阅读快车系列答案 空间存在一沿x轴方向的静电场,电场强度E随x变化的关系如图所示,A、B、C为x轴上的点,取x轴正方向为电场强度的正方向,则下列说法正确的是( )
空间存在一沿x轴方向的静电场,电场强度E随x变化的关系如图所示,A、B、C为x轴上的点,取x轴正方向为电场强度的正方向,则下列说法正确的是( )| A. | AC段中B点的电势最低 | |
| B. | 一带负电的粒子从A点运动到B点电势能减小 | |
| C. | UAB>UBC | |
| D. | 一正电荷仅在电场力作用下从A点运动到C点动能先增大后减小 |
| A. | 重力对物体做功0.2mgh | B. | 物体的动能增加了0.2mgh | ||
| C. | 物体下落前的重力势能是0.2mgh | D. | 物体的机械能减少了0.2mgh |

| A. | 若木块静止,则木块受到的静摩擦力大小等于mg,方向竖直向上 | |
| B. | 若木块静止,当F增大时,木块受到的静摩擦力随之增大 | |
| C. | 若木块沿墙壁向下运动,则墙壁对木块的摩擦力大小为μF | |
| D. | 若开始时木块静止.当撤去F,木块沿墙壁下滑时,木块不受滑动摩擦力作用 |
 一细圆环上均匀分布着负电荷,M、N是圆环轴线上的两个点,它们到圆心O的距离$\overline{MO}$>$\overline{NO}$,M、N两点电场强度大小和电势分别用EM,EN和ΦM,ΦN表示,则( )
一细圆环上均匀分布着负电荷,M、N是圆环轴线上的两个点,它们到圆心O的距离$\overline{MO}$>$\overline{NO}$,M、N两点电场强度大小和电势分别用EM,EN和ΦM,ΦN表示,则( )| A. | EM<EN | B. | EM>EN | C. | ΦM<ΦN | D. | ΦM>ΦN |
| A. | 在匀速运动中,存在加速度且加速度大小和方向均不变 | |
| B. | 在匀速运动中,不存在加速度 | |
| C. | 在变速运动中,存在加速度,且加速度变小时,它的速度也随着变小 | |
| D. | 在变速运动中,存在加速度,且加速度不变时,它的速度也不变 |
 图为某同学改装毫安表的电路图,已知毫安表表头的内阻为100Ω,满偏电流为1mA,R1和R2为阻值固定的电阻.若使用如图电路可以得到量程为3mA和10mA的电流表A1和A2,则:
图为某同学改装毫安表的电路图,已知毫安表表头的内阻为100Ω,满偏电流为1mA,R1和R2为阻值固定的电阻.若使用如图电路可以得到量程为3mA和10mA的电流表A1和A2,则: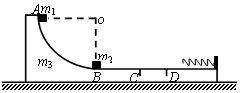 如图所示,质量为m3=2kg的滑道静止在光滑的水平面上,滑道的AB部分是半径为R=1.2m的四分之一圆弧,圆弧底部与滑道水平部分相切,滑道水平部分右端固定一个轻弹簧.滑道除CD部分粗糙外其他部分均光滑.质量为m2=3kg的物体2(可视为质点)放在滑道的B点,现让质量为m1=1kg的物体1(可视为质点)自A点由静止释放.两物体在滑道上的C点相碰后粘为一体(g=10m/s2).求:
如图所示,质量为m3=2kg的滑道静止在光滑的水平面上,滑道的AB部分是半径为R=1.2m的四分之一圆弧,圆弧底部与滑道水平部分相切,滑道水平部分右端固定一个轻弹簧.滑道除CD部分粗糙外其他部分均光滑.质量为m2=3kg的物体2(可视为质点)放在滑道的B点,现让质量为m1=1kg的物体1(可视为质点)自A点由静止释放.两物体在滑道上的C点相碰后粘为一体(g=10m/s2).求: