题目内容
19. 长为L的细线,拴一质量为m的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示.当摆线L与竖直方向的夹角是θ时,
长为L的细线,拴一质量为m的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示.当摆线L与竖直方向的夹角是θ时,求:(1)线的拉力F;
(2)小球运动的线速度的大小;
(3)小球运动的角速度.
分析 小球在重力和摆线的拉力的合力作用下做圆周运动,靠这两个力的合力提供向心力,根据牛顿第二定律求出线的拉力和线速度大小、角速度大小.
解答  解:(1)小球靠重力和拉力的合力提供向心力,根据平行四边形定则知,拉力F=$\frac{mg}{cosθ}$.
解:(1)小球靠重力和拉力的合力提供向心力,根据平行四边形定则知,拉力F=$\frac{mg}{cosθ}$.
(2)根据牛顿第二定律有:$mgtanθ=\frac{m{v}^{2}}{Lsinθ}$,
解得线速度v=$\sqrt{gLtanθsinθ}$,
(3)小球的角速度$ω=\frac{v}{Lsinθ}=\sqrt{\frac{g}{Lcosθ}}$.
答:(1)线的拉力为$\frac{mg}{cosθ}$;
(2)小球运动的线速度大小为$\sqrt{gLtanθsinθ}$;
(3)小球运动的角速度为$\sqrt{\frac{g}{Lcosθ}}$.
点评 本题是圆锥摆问题,关键要正确分析受力,搞清小球做圆周运动向心力的来源:重力和拉力的合力,要注意小球圆周运动的半径不是L,而是Lsinα.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.如下图所示各图线中表示交变电流的是( )
| A. |  | B. |  | C. |  | D. |  |
14.用跨过定滑轮的绳把湖中小船拉靠岸,如图所示,已知拉绳的速度v0保持不变,则船速( )


| A. | 保持不变 | B. | 逐渐增大 | C. | 逐渐减小 | D. | 先增大后减小 |
8. 如图所示,用丝线悬挂闭合金属环,悬于O点,虚线左边有匀强磁场,右边没有磁场.由图所示的位置开始释放金属环,不考虑空气阻力,则下列说法正确的是( )
如图所示,用丝线悬挂闭合金属环,悬于O点,虚线左边有匀强磁场,右边没有磁场.由图所示的位置开始释放金属环,不考虑空气阻力,则下列说法正确的是( )
 如图所示,用丝线悬挂闭合金属环,悬于O点,虚线左边有匀强磁场,右边没有磁场.由图所示的位置开始释放金属环,不考虑空气阻力,则下列说法正确的是( )
如图所示,用丝线悬挂闭合金属环,悬于O点,虚线左边有匀强磁场,右边没有磁场.由图所示的位置开始释放金属环,不考虑空气阻力,则下列说法正确的是( )| A. | 金属环会一直在摆动 | B. | 金属环摆动的高度不变 | ||
| C. | 整个摆动过程一直有热能增加 | D. | 只有摆进或摆出磁场时热能增加 |
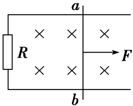 如图所示,匀强磁场磁感应强度B=0.8T,方向垂直轨道平面,导轨间距L=0.5m,拉力F=0.2N,电阻R=4Ω,一切摩擦不计,求:
如图所示,匀强磁场磁感应强度B=0.8T,方向垂直轨道平面,导轨间距L=0.5m,拉力F=0.2N,电阻R=4Ω,一切摩擦不计,求:
 如图所示,质量为M=3kg足够长的长木板放在光滑的水平地面上,另一质量为m=1kg的小物块从长木板的左端以初速度v0=4m/s滑向右端.已知物块与木板间的动摩擦因数μ=0.2,求:
如图所示,质量为M=3kg足够长的长木板放在光滑的水平地面上,另一质量为m=1kg的小物块从长木板的左端以初速度v0=4m/s滑向右端.已知物块与木板间的动摩擦因数μ=0.2,求: