题目内容
5. 如图,细线长为L,一端固定在O点,另一端系一个质量为m的小球.小球在光滑水平面上作角速度为ω的匀速圆周运动,细线伸直,与竖直方向夹角为α.求:
如图,细线长为L,一端固定在O点,另一端系一个质量为m的小球.小球在光滑水平面上作角速度为ω的匀速圆周运动,细线伸直,与竖直方向夹角为α.求:(1)小球与水平面间的压力;
(2)为使小球不离开水平面,角速度ω的最大值为多少?
分析 (1)小球受重力、拉力和支持力作用,竖直方向受力平衡,水平方向的合力提供向心力,根据平衡条件及向心力公式求解;
(2)摆球离开水平面的临界状态:N=0,结合第一问结论求解即可.
解答 解:(1)对小球受力分析,竖直方向受力平衡,水平方向的合力提供向心力,则有:
Tsinα=mω2 Lsinα
Tcosα+N-mg=0
解得:N=mg-Tcosα=mg-mω2 Lcosα
(2)摆球离开水平面的临界状态:N=0,
则 mg=mω2 Lcosα
得$ω=\sqrt{\frac{g}{Lcosα}}$
答:(1)小球与水平面间的压力为mg-mω2 Lcosα;
(2)为使小球不离开水平面,角速度ω的最大值为$\sqrt{\frac{g}{Lcosα}}$.
点评 本题关键是明确球的运动情况和受力情况,找到向心力来源,根据牛顿第二定律列式求解,基础题目.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
15. 如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )
如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )
 如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )
如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )| A. | q一定是正电荷 | B. | q一定是负电荷 | C. | q离Q1比离Q2近 | D. | q离Q1比离Q2远 |
13.下列说法正确的是( )
| A. | 物体从外界吸收热量,其内能一定增加 | |
| B. | 热机的效率可以达到100% | |
| C. | 叶面上的小露珠呈球形是由于液体表面张力的作用 | |
| D. | 布朗运动是悬浮颗粒分子的无规则运动 |
 如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=15m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求:
如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=15m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求: 把质量为5g的带电小球A用细绳吊起来,若将带电小球B靠近带电小球A,当B球带电荷量QB=4×10-6C时,两个带电体恰在同一高度,且相距l=30cm,绳与竖直方向的夹角为45°,如图,试求:
把质量为5g的带电小球A用细绳吊起来,若将带电小球B靠近带电小球A,当B球带电荷量QB=4×10-6C时,两个带电体恰在同一高度,且相距l=30cm,绳与竖直方向的夹角为45°,如图,试求: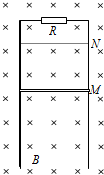 如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻,将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.
如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻,将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.