题目内容
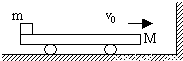
水平光滑的地面上,质量为m的木块放在质量为M的平板小车的左端,M>m,它们一起以大小为v的速度向右做匀速直线运动,木块与小车之间的动摩擦因数为µ,小车与竖直墙碰后立即以v向左运动,m没从M上掉下.求:(1)它们的最后速度?
(2)木块在小车上滑行的时间?
(3)小车至少多长?
【答案】分析:(1)根据动量守恒定律列式求解即可;
(2)对滑块相对与平板的滑动过程运用动量定理列式求解即可;
(3)对小车和滑块系统运用功能关系列式求解.
解答:解:(1)小车与墙壁碰撞后,小车与滑块系统动量守恒,有:(M+m)v=Mv-mv
解得:v=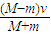 ;
;
(2)滑块相对与平板的滑动过程,根据动量定理,有:µmgt=m(v+v)
解得:t=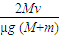
(3)对小车和滑块系统运用功能关系列式,有:
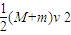 =
=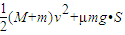
解得:S=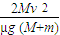
答:(1)它们的最后速度为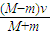 ;
;
(2)木块在小车上滑行的时间为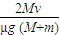 ;
;
(3)小车至少长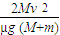 .
.
点评:本题关键是根据动量守恒定律、动量定理、功能关系列式后联立求解,不难.
(2)对滑块相对与平板的滑动过程运用动量定理列式求解即可;
(3)对小车和滑块系统运用功能关系列式求解.
解答:解:(1)小车与墙壁碰撞后,小车与滑块系统动量守恒,有:(M+m)v=Mv-mv
解得:v=
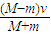 ;
;(2)滑块相对与平板的滑动过程,根据动量定理,有:µmgt=m(v+v)
解得:t=
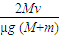
(3)对小车和滑块系统运用功能关系列式,有:
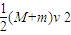 =
=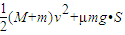
解得:S=
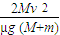
答:(1)它们的最后速度为
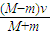 ;
;(2)木块在小车上滑行的时间为
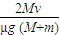 ;
;(3)小车至少长
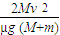 .
.点评:本题关键是根据动量守恒定律、动量定理、功能关系列式后联立求解,不难.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
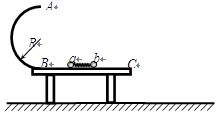
 如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌距水平地面的高度也为R.在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在水平桌面上分离后,a球从B点滑上光滑半圆环轨道并恰能通过半圆环轨道最高点A,b球则从桌面C点滑出后落到水平地面上,落地点距桌子右侧的水平距离为
如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌距水平地面的高度也为R.在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在水平桌面上分离后,a球从B点滑上光滑半圆环轨道并恰能通过半圆环轨道最高点A,b球则从桌面C点滑出后落到水平地面上,落地点距桌子右侧的水平距离为 (2011?惠州二模)如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌面距水平地面的高度也为R,在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在桌面上分离后,a球从B点滑上光滑半圆环轨道最高点A时速度为
(2011?惠州二模)如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌面距水平地面的高度也为R,在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在桌面上分离后,a球从B点滑上光滑半圆环轨道最高点A时速度为 如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌面距水平地面的高度也为R,在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在水平桌面上分离后,a球从B点滑上光滑半圆环轨道并恰能通过半圆环轨道最高点A,b球则从桌面C点滑出后落到水平地面上,落地点距桌子右侧的水平距离为
如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌面距水平地面的高度也为R,在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在水平桌面上分离后,a球从B点滑上光滑半圆环轨道并恰能通过半圆环轨道最高点A,b球则从桌面C点滑出后落到水平地面上,落地点距桌子右侧的水平距离为 .已知小球a质量为m,重力加速度为g.求:
.已知小球a质量为m,重力加速度为g.求:
 .已知小球a质量为m,重力加速度为g.求:
.已知小球a质量为m,重力加速度为g.求: