题目内容
20.如图所示,在海边的沙滩上,堆积一个斜坡,可看成一个斜面,一个小孩从斜坡上的A点由静止开始下滑,经过B点后进入水平面(假设经过B点前后速度大小不变),最后停在C点,每隔2s小孩的瞬时速度记录在如表中,重力加速g=10m/s2,求:
| t/s | 0 | 2 | 4 | 6 |
| v/(m/s) | 0 | 8.0 | 14.7 | 9.7 |
(2)小孩从A点滑到C点的总路程和时间(计算结果保留两位有效数字).
分析 (1)由表格中的数据根据加速度的定义式分别求AB段和BC段的加速度,小孩在BC段根据牛顿第二定律求出小孩与沙子之间的动摩擦因数
(2)根据运动学公式求出小孩从A到B的时间和到达B点的速度,再由速度时间关系式求出小孩在BC段的时间,根据平均速度公式$x=\frac{{v}_{0}^{\;}+v}{2}t$求AB和BC段的位移,即可求出总路程和时间
解答 解:(1)由表格知:0~2s内小孩小孩一定在AB段做匀加速运动,加速度大小为:${a}_{1}^{\;}=\frac{{v}_{2}^{\;}-0}{2s}=4m/{s}_{\;}^{2}$
4~6s内小孩一定在BC段做匀减速运动,加速度大小为:${a}_{2}^{\;}=\frac{{v}_{4}^{\;}-{v}_{6}^{\;}}{2s}=2.5m/{s}_{\;}^{2}$
设小孩质量为m,在BC段,根据牛顿第二定律:$μmg=m{a}_{2}^{\;}$
可得:μ=0.25
(2)假设小孩从A点运动到B点的时间是${t}_{1}^{\;}$,那么到4s末时小孩在BC段减速运动的时间为:${t}_{减}^{\;}=4s-{t}_{1}^{\;}$,
故有:${v}_{4}^{\;}={a}_{1}^{\;}{t}_{1}^{\;}-{a}_{2}^{\;}{t}_{减}^{\;}$
解得:${t}_{1}^{\;}=3.8s$
此时速度为:${v}_{1}^{\;}={a}_{1}^{\;}{t}_{1}^{\;}=15.2m/s$
滑行的路程为:${x}_{1}^{\;}=\frac{1}{2}{v}_{1}^{\;}{t}_{1}^{\;}=28.88m$
假设小孩从B点运动到C点的时间是${t}_{2}^{\;}$,则有:${v}_{1}^{\;}-{a}_{2}^{\;}{t}_{2}^{\;}=0$,
解得:${t}_{2}^{\;}=6.08s$
滑行的路程为:${x}_{2}^{\;}=\frac{1}{2}{v}_{1}^{\;}{t}_{2}^{\;}=46.208m$
故总路程为:$x={x}_{1}^{\;}+{x}_{2}^{\;}≈75m$
总时间为:$t={t}_{1}^{\;}+{t}_{2}^{\;}≈9.9s$
答:(1)小孩在AB段加速度大小为$4m/{s}_{\;}^{2}$和BC段的加速度大小$2.5m/{s}_{\;}^{2}$及小孩与沙子之间的动摩擦因数0.25;
(2)小孩从A点滑到C点的总路程75m和时间9.9s.
点评 本题考察一个物体参与多个过程的情况,对于这类问题要弄清各个过程的运动形式,然后根据相应的运动学公式求解.

 同步轻松练习系列答案
同步轻松练习系列答案| A. | 起重机的拉力相等,功率不等 | B. | 起重机的拉力相等,功率也相等 | ||
| C. | 两次重力做功相等 | D. | 起重机拉力相等,拉力做功也相等 |
| A. | 波速表示振动在介质中传播的快慢 | B. | 波速表示介质质点振动的快慢 | ||
| C. | 波速表示介质质点迁移的快慢 | D. | 波速跟波源振动的快慢无关 |

| A. | 打点计时器应接交流电源 | B. | 本实验应该用天平测出重锤的质量 | ||
| C. | 需使用秒表测出重锤下落的时间 | D. | 应先松开纸带后通电源 |
| A. | 整个运动过程中,汽车运动的最大速度是v | |
| B. | 整个运动过程中,汽车运动的最大速度$\frac{m{v}^{2}}{ft}$ | |
| C. | 匀加速运动阶段,汽车的牵引力为f+m$\frac{v}{t}$ | |
| D. | 汽车的额定功率为(m$\frac{v}{t}$+f)v |
 如图所示,空间存在磁感应强度为B=2T的匀强磁场.单砸矩形线框abcd绕ab为轴以角速度ω=20π弧度/秒逆时针转动.已知ab=bc=20cm.线框回路总电阻为R=2Ω.求:
如图所示,空间存在磁感应强度为B=2T的匀强磁场.单砸矩形线框abcd绕ab为轴以角速度ω=20π弧度/秒逆时针转动.已知ab=bc=20cm.线框回路总电阻为R=2Ω.求: 如图所示,质量为M=8kg的木板,放在水平地面上,木板向右运动的速度v0=5m/s时,在木板前端轻放一个大小不计,质量为m=2kg的小物块.木板与地面、物块与木板间的动摩擦因数均为μ=0.2,g=10m/s2,求:
如图所示,质量为M=8kg的木板,放在水平地面上,木板向右运动的速度v0=5m/s时,在木板前端轻放一个大小不计,质量为m=2kg的小物块.木板与地面、物块与木板间的动摩擦因数均为μ=0.2,g=10m/s2,求: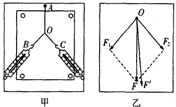 “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.