题目内容
 如图以y轴为边界,右边是一个水平向左的E1=1×104N/C匀强电场,左边是一个与水平方向成45°斜向上的E2=
如图以y轴为边界,右边是一个水平向左的E1=1×104N/C匀强电场,左边是一个与水平方向成45°斜向上的E2=
| ||
| 2 |
(1)第一次经过y轴时的坐标及时间
(2)第二次经过y轴时的坐标
(3)第二次经过y轴时小颗粒的速度大小.
分析:本题(1)的关键是通过求出小颗粒受到的重力与电场力相等可知小颗粒受到的合力以及合力的方向,从而根据牛顿运动定律可求出第一次经过y轴时的坐标与时间.题(2)的难点在于小颗粒进入电场
后求出电场力,且电场力与重力的合力正好与小颗粒的速度方向垂直,即小颗粒将做类平抛运动,然后再按类平抛的规律即可求解.(3)题的关键是由于要求的速度大小,所以可以利用动能定理求解.
| E | 2 |
解答:解:(1小颗粒在
中电场力为
=
q=0.01N,重力G=mg=0.01N,所以合力
=
mg,合力方向指向原点,即小颗粒向原点做匀加速直线运动,所以第一次经过Y轴的坐标为(0,0),加速度为a=
=10
m/
,又位移s=
×0.1m=0.1
由s=
可得t=0.1
s
故第一次经过y轴时的坐标为(0,0),时间为0.1
s.
(2)小颗粒在
中受到的电场力为
=q
=
N,将重力mg沿小颗粒速度方向及与垂直于速度的方向正交分解,则在沿速度方向的合力大小为
=mgsin45°-q
=0,在垂直于速度方向的合力为
=mgcos45°=
N,由此可得小颗粒做类平抛运动,设再次运动到y轴的时间为
,则在沿速度方向的位移为
=
=(at)
=10
×0.1
=2
沿垂直于速度方向的位移为
=
=
=
再由几何关系得
联立解得
=
=0.8
m
所以第二次经过y轴时到运动的距离外L=
=1.6m,即坐标为(0,-1.6)
故第二次经过y轴时的坐标为(0,-1.6).
(3)根据动能定理得FLcos45=
-
,解得v=2
m/s,故第二次经过y轴上小颗粒的速度大小为2
m/s.
| E | 1 |
| F | 1 |
| E | 1 |
| F | 合 |
| 2 |
| ||
| m |
| 2 |
| s | 2 |
| 2 |
| 2m |
由s=
| 1 |
| 2 |
| at | 2 |
| 2 |
故第一次经过y轴时的坐标为(0,0),时间为0.1
| 2 |
(2)小颗粒在
| E | 2 |
| F | 2 |
| E | 2 |
0.01
| ||
| 2 |
| F | 平行 |
| E | 2 |
| F | 垂直 |
0.01
| ||
| 2 |
| t | 1 |
| x | 1 |
| 1 |
| t | 1 |
| 2 |
| 2 |
| t | 1 |
| t | 1 |
沿垂直于速度方向的位移为
| y | 1 |
| 2 1 |
| 1 |
| 2 |
| 2 1 |
5
| ||
| 2 |
| t | 2 1 |
再由几何关系得
| x | 1 |
| =y | 1 |
联立解得
| x | 1 |
| y | 1 |
| 2 |
所以第二次经过y轴时到运动的距离外L=
| 2 |
| x | 1 |
故第二次经过y轴时的坐标为(0,-1.6).
(3)根据动能定理得FLcos45=
| ||
| 2 |
| ||
| 2 |
| 5 |
| 5 |
点评:遇到动力学问题关键是正确进行受力分析和运动过程分析,然后选择相应的物理规律列式求解即可.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 (2011?青铜峡市一模)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度V0沿x轴正方向开始运动,已知P点的坐标为(-L,0)且
(2011?青铜峡市一模)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度V0沿x轴正方向开始运动,已知P点的坐标为(-L,0)且 (2007?河东区模拟)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界.现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,0)处,以初速度v0沿x轴正方向开始运动,且已知
(2007?河东区模拟)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界.现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,0)处,以初速度v0沿x轴正方向开始运动,且已知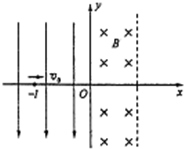 如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界线,图中虚线为磁场区域的右边界,现有一质量为m、电荷量为-q的带电粒子从电场中坐标位置(-l,0)处,以初速度v0沿x轴正方向开始运动,且已知
如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界线,图中虚线为磁场区域的右边界,现有一质量为m、电荷量为-q的带电粒子从电场中坐标位置(-l,0)处,以初速度v0沿x轴正方向开始运动,且已知