题目内容
8. 如图所示,半径为R的光滑的$\frac{3}{4}$圆弧轨道AC放在竖直平面内,与足够长的粗糙水平轨道BD通过光滑水平轨道AB相连,在光滑水平轨道上,有a、b两物块和一段轻质弹簧.将弹簧压缩后用细线将它们拴在一起,物块与弹簧不拴接.将细线烧断后,物块a通过圈弧轨道的最高点P时,对轨道的压力等于自身重力.已知物块a的质量为m,b的质量为2m,物块b与BD面间的动摩擦因数为μ,物块到达A点或B点前已和弹簧分离,重力加速度为g.求:
如图所示,半径为R的光滑的$\frac{3}{4}$圆弧轨道AC放在竖直平面内,与足够长的粗糙水平轨道BD通过光滑水平轨道AB相连,在光滑水平轨道上,有a、b两物块和一段轻质弹簧.将弹簧压缩后用细线将它们拴在一起,物块与弹簧不拴接.将细线烧断后,物块a通过圈弧轨道的最高点P时,对轨道的压力等于自身重力.已知物块a的质量为m,b的质量为2m,物块b与BD面间的动摩擦因数为μ,物块到达A点或B点前已和弹簧分离,重力加速度为g.求:(1)物块b沿轨道BD运动的距离x;
(2)烧断细线前弹簧的弹性势能Ep.
分析 (1)弹簧弹开a、b过程,ab系统动量守恒,物块a通过轨道最高点P点,由合力充当向心力,由向心力公式可得出小球a在P点的速度,由机械能守恒可得出a球经过A点的速度,进而求得b被弹开时的速度,再根据动能定理求解距离x;
(2)释放弹簧,ab被弹出的过程,由机械能守恒可得出弹簧的弹性势能.
解答 解:(1)弹簧弹开a、b过程,由动量守恒定律得:0=mv1-2mv2
物块a从A到P运动的过程中,由机械能守恒定律得:$\frac{1}{2}m{v}_{1}^{2}=mg•2R+\frac{1}{2}m{v}_{c}^{2}$
在最高点重力与支持力合力提供向心力:$mg+F=m\frac{{v}_{c}^{2}}{R}$
联立可解得:${v}_{1}=\sqrt{6gR}$,${v}_{2}=\frac{\sqrt{6gR}}{2}$
物块b减速到停下的过程中,由动能定理得:$-μ•2mgx=0-\frac{1}{2}•2m{v}_{2}^{2}$
可解得:$x=\frac{3R}{4μ}$
(2)弹簧弹开物块过程,弹性势能转化为动能:${E}_{p}=\frac{1}{2}m{v}_{1}^{2}+\frac{1}{2}•2m{v}_{2}^{2}$
解得弹性势能:${E}_{p}=\frac{9}{2}mgR$
答:(1)物块b沿轨道BD运动的距离x为$\frac{3R}{4μ}$;
(2)烧断细线前弹簧的弹性势能Ep为$\frac{9}{2}mgR$.
点评 本题主要考查了动量守恒定律、动能定理的综合应用,解决本题的关键:一要明确小球a到达圆轨道最高点:合力充当向心力.二要明确有摩擦时往往运用动能定理或能量守恒定律求解.

练习册系列答案
相关题目
20.下列关于历史上物理学家对规律研究的说法,正确的是( )
| A. | 爱因斯坦对光电效应规律的研究说明:光电子的最大初动能与入射光束的能量有关 | |
| B. | 阴极射线及电子的发现说明了原子核具有复杂的结构 | |
| C. | 卢瑟福等科学家利用人工核反应实验,证明了原子核的基本成份是中子和质子 | |
| D. | 玻尔用“量子化”观点,解释了所有原子跃迁时辐射光子(或吸收光子)的规律 |
3.下列对几种物理现象的解释中,正确的是( )
| A. | 砸钉子时不用橡皮锤,只是因为橡皮锤太轻 | |
| B. | 动量相同的两个物体受到相同的制动力的作用,两个物体将同时停下来 | |
| C. | 在推车时推不动是因为推力的冲量为零 | |
| D. | 跳高时在沙坑里填沙,是为了减小冲量 |
13. 如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )
如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )
 如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )
如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )| A. | 重力的冲量 | B. | 合力的冲量 | ||
| C. | 刚到达底端时的动量 | D. | 刚到达底端时的动能 |
20.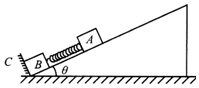 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )
 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )| A. | 弹簧对物块A做功为零 | |
| B. | A、B与弹簧组成的系统机械能守恒 | |
| C. | 物块A、B的质量满足2mgsinθ=kd | |
| D. | 弹簧的弹性势能的减小量为mdgsinθ+$\frac{1}{2}$mv2 |

 甲、乙、丙、丁是四个长度、横截面积均相同的金属导体,某同学对它们各进行了一次测量,把每个导体中通过的电流和两端的电压在I-U坐标系中描点,如图所示,四个导体中电阻率最大的是( )
甲、乙、丙、丁是四个长度、横截面积均相同的金属导体,某同学对它们各进行了一次测量,把每个导体中通过的电流和两端的电压在I-U坐标系中描点,如图所示,四个导体中电阻率最大的是( ) 如图所示.竖直放置的间距为L=1米的两平行光滑导轨,上端连接一个阻值为R=1Ω的电阻,在导轨的MN位置以下有垂直纸面向里的磁场,在MN处的磁感应强度为B0=1T,在MN下方的磁场沿Y轴方向磁感应强度均匀减少,在MN下方1米处的磁感应强度刚好为零.现有一质量为1kg,电阻也是R=1Ω的金属棒,从距离MN为h=0.2米的上方紧贴导轨自由下落,然后进入磁场区域继续下落相同高度h的过程中,能使得电阻R上的电功率保持不变(不计一切摩擦)求(g=10m/s2):
如图所示.竖直放置的间距为L=1米的两平行光滑导轨,上端连接一个阻值为R=1Ω的电阻,在导轨的MN位置以下有垂直纸面向里的磁场,在MN处的磁感应强度为B0=1T,在MN下方的磁场沿Y轴方向磁感应强度均匀减少,在MN下方1米处的磁感应强度刚好为零.现有一质量为1kg,电阻也是R=1Ω的金属棒,从距离MN为h=0.2米的上方紧贴导轨自由下落,然后进入磁场区域继续下落相同高度h的过程中,能使得电阻R上的电功率保持不变(不计一切摩擦)求(g=10m/s2):