题目内容
16. 如图所示为水平传送带装置的示意图,绷紧的传送带始终保持3.0m/s的恒定速率运行,传送带的水平部分AB距离水平地面的高度h=0.45m.现有一煤块(可视为质点)由A端被传送到B端,并被水平抛出,不计空气阻力,取g=10m/s2.
如图所示为水平传送带装置的示意图,绷紧的传送带始终保持3.0m/s的恒定速率运行,传送带的水平部分AB距离水平地面的高度h=0.45m.现有一煤块(可视为质点)由A端被传送到B端,并被水平抛出,不计空气阻力,取g=10m/s2.(1)若煤块从B端水平抛出时的速度v=3.0m/s,求它在空中运动的时间和飞行的水平距离;
(2)在(1)中情况下,煤块落地时的速度大小为多少?若煤块质量为0.2kg,求从A端由静止开始被加速后,摩擦力对煤块所做的功;
(3)若煤块以v0=1.0m/s的初速度从A端向右滑行,煤块与传送带间的动摩擦因数μ=0.20.已知煤块最终仍以v=3.0m/s的速度被水平抛出,求煤块在被抛出前在传送带上留下的痕迹的长度.
分析 (1)煤块做平抛运动,利用运动学公式即可求得;
(2)利用运动学公式和动能定理即可求得;
(3)由牛顿第二定律求的加速度,利用运动学公式即可求得痕迹
解答 解:(1)物体做平抛运动,在竖直方向有:h=$\frac{1}{2}g{t}^{2}$
t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.45}{10}}s=0.3s$
水平方向的位移为:x=vt=3×0.3m=0.9m
(2)在竖直方向获得的速度为:vy=gt=3m/s
故落地速度为:$v′=\sqrt{{v}^{2}{+v}_{y}^{2}}=\sqrt{{3}^{2}+{3}^{2}}m/s=3\sqrt{2}m/s$
有动能定理可得:W=$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}×0.2×{3}^{2}J$=0.9J
(3)煤块产生的加速度为:a=$\frac{μmg}{m}=μg=2m/{s}^{2}$
达到传送带速度所需时间为:t′=$\frac{v-{v}_{0}}{a}=\frac{3-1}{2}s=1s$
各自前进的位移为:x=vt′=3×1m=3m
$x′={v}_{0}t′+\frac{1}{2}at{′}^{2}=2m$
故轨迹为:△x=x-x′=1m
答:(1)它在空中运动的时间为0.3s,飞行的水平距离为0.9m
(2)块落地时的速度为3$\sqrt{2}m/s$,做功为0.9J
(3)煤块在被抛出前在传送带上留下的痕迹的长度为1m.
点评 本题主要考查了运动学公式和牛顿第二定律,加速度是解决问题的关键

练习册系列答案
相关题目
6.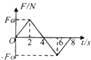 一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
 一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )| A. | 在0-2s内质点做匀加速运动,第2s末其速度达到最大值 | |
| B. | 第4s末质点的加速度为零,速度也刚好为零 | |
| C. | 质点做变加速直线运动,第6s末加速度最大,且离出发位置最远 | |
| D. | 在0-8s内,质点一直向同一个方向做直线运动,在第8s末速度和加速度都为零,且离出发点最远 |
7.物理学中,科学家处理物理问题用到了多种思想与方法,根据你对物理学的学习,关于科学家的思想和贡献,下列说法正确的是( )
| A. | 伽利略猜想做自由落体运动的物体,其下落的距离与时间成正比,并用实验进行了验证 | |
| B. | 牛顿首先提出“提出假说,数学推理,实验验证,合理外推”的科学推理方法 | |
| C. | 赫兹首次用实验证实了电磁波的存在 | |
| D. | 麦克斯韦提出了狭义相对论 |
4.若规定向正东为位移的正方向,今有一个皮球停在水平面的某处,轻踢它一脚,使它向正东做直线运动,运动5m远与墙相碰,后又向正西做直线运动,运动7m后停下.则上述过程中皮球通过的路程和位移分别是( )
| A. | 12m、2m | B. | 12m、-2m | C. | -2m、2m | D. | 2m、-2m |
11.在以下的现象中,属于静电防止的是( )
| A. | 静电复印 | |
| B. | 在以煤为燃料的工厂的烟囱中加装电极除尘 | |
| C. | 静电喷漆 | |
| D. | 油罐车用铁链拖地而行 |
1. 2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
 2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )| A. | sin3θ | B. | $\frac{1}{si{n}^{3}θ}$ | C. | $\sqrt{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |
8.下列说法正确的是( )
| A. | 只要知道水的摩尔质量和水分子的质量,就可以计算出阿伏伽德罗常数 | |
| B. | 空气相对湿度越大时,空气中水蒸气压强越接近饱和气压,水蒸发越快 | |
| C. | 液体表面张力的方向与液面垂直并指向液体内部 | |
| D. | 利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的. |
6.物体从A静止出发,做匀加速直线运动,紧接着又做匀减速直线运动,到达B点时恰好停止.在先后两个运动过程中( )
| A. | 物体通过的路一定相等 | B. | 两次运动的加速度大小一定相同 | ||
| C. | 平均速度一定相同 | D. | 所用的时间一定相同 |
 某同学用图示的装置来验证加速度和质量成反比,在自制的双层架子上固定平板玻璃,架子放在水平桌面上,连接小车的细绳跨过定滑轮与小桶相连,实验步骤如下:
某同学用图示的装置来验证加速度和质量成反比,在自制的双层架子上固定平板玻璃,架子放在水平桌面上,连接小车的细绳跨过定滑轮与小桶相连,实验步骤如下: