题目内容
5. 某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5W工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,s=1.50m.问要使赛车完成比赛,
某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5W工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,s=1.50m.问要使赛车完成比赛,(1)在竖直圆轨道最高点速度至少为多大?
(2)在竖直圆轨道最低点B赛车对轨道压力至少为多大?
(3)电动机至少工作多长时间?(取g=10m/s2)
分析 (1)赛车刚好到达竖直圆轨道最高点时,由重力提供向心力,根据牛顿第二定律求赛车通过圆轨道最高点的最小速度.
(2)竖直圆轨道是光滑的,由动能定理求出小球通过B点的最小速度,再由牛顿定律求在竖直圆轨道最低点B赛车对轨道压力的最小值.
(3)通过平抛运动的规律求出赛车通过B点的速度,从而确定通过B点的最小速度,根据动能定理求出要使赛车完成比赛,电动机至少工作的时间.
解答 解:(1)设赛车恰好到达最高点时速度为v′1.根据牛顿第二定律得,mg=m$\frac{{v}_{1}^{′2}}{R}$,则得 v′1=$\sqrt{gR}$=$\sqrt{10×0.32}$=$\frac{4\sqrt{5}}{5}$m/s
所以赛车在竖直圆轨道最高点速度至少为$\frac{4\sqrt{5}}{5}$m/s.
(2)赛车从B到竖直圆轨道最高点的过程,根据动能定理得
-mg•2R=$\frac{1}{2}$m${v}_{1}^{′2}$-$\frac{1}{2}m{v}_{1}^{2}$
解得,赛车要通过圆轨道最高点到达B点的速度至少为 v1=$\sqrt{5gR}$=$\sqrt{5×10×0.32}$=4m/s
在B点,由牛顿第二定律得
N-mg=m$\frac{{v}_{1}^{2}}{R}$
联立得 N=6mg=6×0.1×10=6N
由牛顿第三定律得知,在竖直圆轨道最低点B赛车对轨道压力至少为 N′=N=6N
(3)赛车恰好能越过壕沟时,根据平抛运动规律有
h=$\frac{1}{2}g{t}^{2}$
得,t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×1.25}{10}}$=0.5s
则平抛运动的初速度 v2=$\frac{s}{t}$=$\frac{1.5}{0.5}$=3m/s.
综上,为保证越过壕沟,到达B点的速度至少为 v1=4m/s
因此赛车到达B点的速度至少为:v=v1=4m/s
从A到B对赛车用动能定理:
Pt′-fL=$\frac{1}{2}$mv12
解得 t′=2.54s
答:
(1)在竖直圆轨道最高点速度至少为$\frac{4\sqrt{5}}{5}$m/s.
(2)在竖直圆轨道最低点B赛车对轨道压力至少为4m/s.
(3)电动机至少工作2.54s时间.
点评 解决本题的关键要把握圆周运动最高点的临界条件:重力等于向心力.掌握平抛运动的规律,在已知水平距离和下落高度时,要求得平抛运动的初速度.

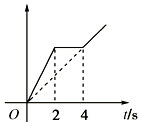 如图所示,表示某一物体的运动图象,由于画图人粗心未标明是v-t图象还是x-t图象,但已知第1s内的速度比第3s内的速度大,下列说法正确的是( )
如图所示,表示某一物体的运动图象,由于画图人粗心未标明是v-t图象还是x-t图象,但已知第1s内的速度比第3s内的速度大,下列说法正确的是( )| A. | 该图一定是v-t图象 | B. | 该图一定是x-t图象 | ||
| C. | 前2s物体的速度越来越大 | D. | 前2s物体的位移越来越大 |
| A. | α粒子流 | B. | 质子流 | C. | 中子流 | D. | 电子流 |
| A. | 没有力作用,物体只能处于静止状态 | |
| B. | 物体抵抗运动状态变化的性质是惯性 | |
| C. | 行星在圆周轨道上保持匀速率运动的性质是惯性 | |
| D. | 运动物体如果没有受到力的作用,物体可能做匀速圆周运动 |
 如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )
如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )| A. | 金属板A为电源的正极 | |
| B. | 开关断开时,金属板间的电势差为Bvd | |
| C. | 开关闭合后,金属板间的电势差为$\frac{BvdR}{R+r}$ | |
| D. | 等离子体发生偏转的原因是洛伦兹力大于所受电场力 |
 如图所示,在水平地面上有一质量为2m、倾角为θ、上表面粗糙的斜面体B,其上放置一质量为m的物体A.B与地面的动摩擦因数为μ.若对B施加一水平推力F,使A与B一起向左运动,重力加速度为g,则:
如图所示,在水平地面上有一质量为2m、倾角为θ、上表面粗糙的斜面体B,其上放置一质量为m的物体A.B与地面的动摩擦因数为μ.若对B施加一水平推力F,使A与B一起向左运动,重力加速度为g,则: